【 問 題 】

　ＡチームとＢチームが４０戦したところ、 Ａチームの２２勝１８敗であった。（ これを事実Ｗとする。） それも、 初戦から最終戦まで終始単独首位をキープした。（ これを事実Ｑとする。） このことから、 ＡチームはＢチームよりも戦力が勝っているといえるか？　危険率５％で答えよ。

【 解 答 】

　ＡチームとＢチームの戦力は等しいと仮定して、 事実Ｗが起こる確率を求める。 それが５％以下であれば、 危険率５％でＡチームはＢチームよりも戦力が勝っていると言い切ることができる。

Ａチームの勝ち負けの順番のパターンは全部で、
　　　₄₀Ｃ₂₂　通り　　・ ・ ・ ・　
事実Ｑとなる場合の数は、
　　　₃₉Ｃ₂₁ − ₃₉Ｃ₂₂　通り　　・ ・ ・ ・　

の理由 ：
　事実Ｑとなる場合とは 、初戦で １ 勝し、 その後に一度も同率首位になることなく事実Ｗが起こる場合のことである。

　　₃₉Ｃ₂₁ ：　初戦で １ 勝して事実Ｗが起こる場合の数
　　₃₉Ｃ₂₂ ：　初戦で １ 敗して事実Ｗが起こる場合の数

　 横軸に対戦数をとり、 縦軸にＡチームの勝ち超し数をとった折れ線グラフを作る。 初戦で １ 勝しその後に同率首位になってから事実Ｗが起こるケースについては、 最初から一番最後に同率首位になるまでの区間を横軸に対しての鏡像に置き換えると、 初戦で １ 敗して事実Ｗが起こるケースになる。 これらは １：１ の対応になっているので、 初戦で １ 敗して事実Ｗが起こる場合の数は、 初戦で １ 勝しその後に同率首位になってから事実Ｗが起こる場合の数に等しい。 事実Ｑが起こる場合の数は、 初戦で １ 勝して事実Ｗが起こる場合の数 から 初戦で １ 勝しその後に同率首位になってから事実Ｗが起こる場合の数 を引いて求めることができるので、 事実Ｑが起こる場合の数は の式で表される。

₃₉Ｃ₂₁ − ₃₉Ｃ₂₂
　　　＝ （ 39・38・37・・・・20・19 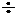） （ 21・20・19・・・・3・2 ）
　　　　　　　　　　− （ 39・38・37・・・・19・18 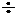） （ 22・21・20・・・・3・2 ）
　　　＝ （ 39・38・37・・・・20・19・4 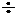） （ 22・21・20・・・・3・2 ）

₄₀Ｃ₂₂　＝ （ 40・39・38・37・・・・20・19 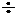） （ 22・21・20・・・・3・2 ）

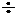
　＝→　4 / 40 　＝→　1 / 10　＝→　10 ％

10 ％ が事実Ｑが起こる確率である。
したがって、 危険率５％で、 ＡチームはＢチームよりも戦力が勝っていると言い切ることはできない。


シミュレーション ：


　戦力が同等な Ａチーム と Ｂチーム のリーグ戦。
　４０戦して、 Ａチームの 22 勝 18 敗。
　この間、 終始単独 １ 位であった。
　22 勝 18 敗 の条件下で、 終始単独首位になる確率はいくらか？

　　　　　

　　　　　　Ａチームの 22 勝 18 敗 となったのは、 10万回試行のうち 回
　　　　　　求める確率 ：　 %　　（ 理論値 ＝ 10 % ）


プログラムの内容 ：