Ａ君とＢ君が常に同じ距離を保ちながら正面を向き合っています。
Ａ君の座標系では、Ｂ君は原点を見つめたまま 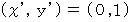に静止しています。
Ｂ君の座標系では、Ａ君は原点を見つめたまま 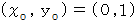に静止しています。

Ａ君と同じ場所には自転していないＡ' さんがいます。
Ｂ君と同じ場所には自転していないＢ' さんがいます。
Ａ君とＢ君を結ぶ中点には自転していないＣさんがいます。

　 Ａ' さんからすると、 Ｂ君はＡ君の周りを 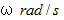の速さで反時計回りに等速円移動しています。 また、 Ａ君もＢ君も 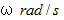の速さで反時計回りに自転しています。

　 Ａ' さんからすると、 Ａ君の座標系は 「 等速自転座標系 （ 一般的には等速回転座標系と言われる ）」であり、 Ｂ君の座標系は 「 等速自公転座標系 （ 私の造語 ） 」 です。

　 Ａ' さんの座標系における時刻 ｔ でのＢ君の位置は 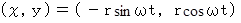です。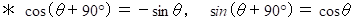
　　　　　　　　　　　　
　 Ａ君の座標系では、 Ｂ君の速度や加速度は０です。 Ａ' さんからするとＡ君の座標は等速自転座標系になります。 そこで、 等速自転座標系における加速度の公式を用いて、 Ａ君の座標系ではＢ君の加速度が０であることを確かめてみましょう。

　　等速自転座標系における質点の加速度 ：
　　　　　

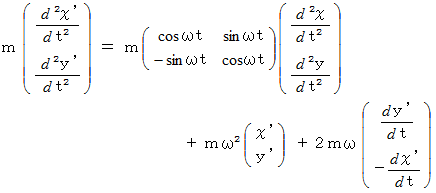
　　Ａ君の等速自転座標系におけるＢ君の運動データーは次のようになります。
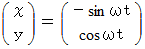　　　　　　より、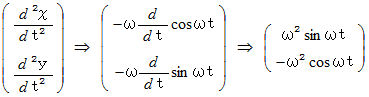
　　　　　
　　　　　
　　　　　

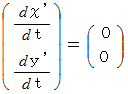
　　したがって、 Ａ君の等速自転座標系におけるＢ君の運動方程式は次のようになります。
　　　　　


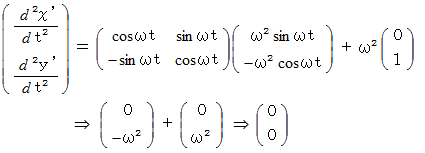
　 さて、 このとき、 Ｂ' さんからすると、 Ａ君はＢ君の周りを 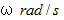の速さで反時計回りに等速円運動しています。 また、 Ａ君もＢ君も 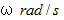の速さで反時計回りに自転しています。 ということは、 Ｂ' さんが見るＡ君の運動 は Ａ' さんが見るＢ君の運動 と同じであるということです。 Ｂ' さんからするとＢ君の座標は等速自転座標系であり、 Ａ君の座標は 「 等速自公転座標系 」 になります。 このことを 「 自転座標系 と 自公転座標系 との相対性 」 と言うことにしましょう。
　また、 このとき、 Ｃさんからすると、 Ａ君もＢ君もＣさんの周りを 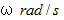の速さで反時計回りに等速円運動していて、 かつ、 Ａ君もＢ君も 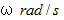の速さで反時計回りに自転しています。