（１）主成分分析のイメージ

　４つの点ＡＢＣＤが半径５の同円周上にあります。ＡＢ＝６，ＡＤ＝８，ＢＤ＝10 です。これらの位置ベクトルの総和は０です。４点を結ぶと長方形になります。

　　図-１
　　　　
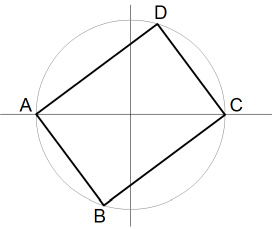
　　　　　　Ａ( −5, 0 )　Ｂ( −7/5, −24/5 )　Ｃ( 5, 0 )　Ｄ( 7/5, 24/5 )

　この図を回転させたときに、点Ａ〜点Ｄの x 座標値の分散（ 平均値からのへだたりの２乗の平均 ）が最高になるのはどんなときでしょうか？ それは次の図のようになるときです。

　　図-２
　　　　
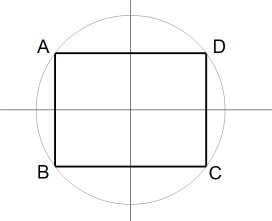
　　　　　　Ａ( −4, 3 )　Ｂ( −4, −3 )　Ｃ( 4, −3 )　Ｄ( 4, 3 )

　以上が主成分分析のイメージです。主成分分析とは、分析というより相関関係のあるデーターの加工です。見やすくて利用しやすくなるようにデーターを加工することです。図２の横軸（ x 軸 ）が第１主成分、縦軸（ y 軸 ）が第２主成分です。

　相関関係の象徴がベクトルの内積です。特に大きさが１のベクトルどうしの内積は相関係数に匹敵します。下記のものは内積行列です。
　　　　

（２）主成分分析は何をしているのか？

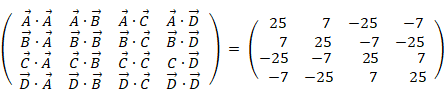
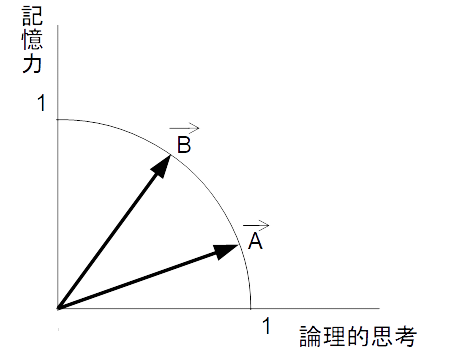
　数学には、論理的思考力が 67.4%、記憶力が 32.6% 必要です。歴史には、論理的思考力が 32.6%、記憶力が 67.4% 必要です。必要とされる知能の観点から、この２つの教科の相関係数を求めてみましょう。それには、論理的思考力を横軸とし記憶力を縦軸とする座標系の中で、数学知能ベクトル と 歴史知能ベクトル をそれぞれ大きさ１のベクトルで表し、その２つの内積をとればいいのです。
　　　数学知能ベクトル ( 0.9, 0.436 )
　　　歴史知能ベクトル ( 0.436, 0.9 )
　　　　　　　※ 0.9 ² ＋ 0.436 ² ＝ 1
　　　　　　　※ 0.9 / ( 0.9 ＋ 0.436 ) ＝ 0.674

　　　　　　　　
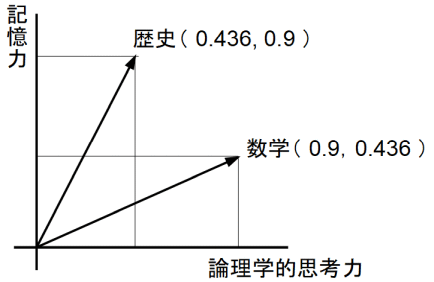
　　　２つのベクトルの内積は、0.78 です。

相関行列：
　　
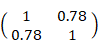
　　相関行列の固有値と大きさ１の固有ベクトル:
　　　　固有値 1.78；　( 0.707, 0.707 )　← これは傾き45°のベクトルである。
　　　　固有値 0.22；　( 0.707, −0.707 )　← 上記のベクトルに直交する。

　甲さんと乙さんの数学と歴史の２つの教科のテストの年間平均点は次のようになっています。

	数 学	歴 史
甲さん	90 点	70 点
乙さん	50 点	70 点


　　　　　甲さんのテスト結果ベクトル ( 90, 70 )
　　　　　乙さんのテスト結果ベクトル ( 50, 70 )

　　　　　　　　


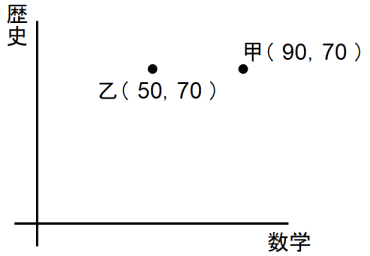
　さて、先ほど示した相関行列を表現行列とするテンソルにより、甲さんのテスト結果ベクトル は 甲さんの知能ベクトル へと変換され、乙さんのテスト結果ベクトル は 乙さんの知能ベクトル へと変換されます。
　　　
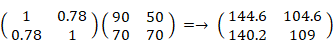
そして、それらはそれぞれ次のようになります。
　　　甲さんの知能ベクトル ( 144.6, 140.2 )
　　　乙さんの知能ベクトル ( 104.6, 109 )

　　　　　　　　

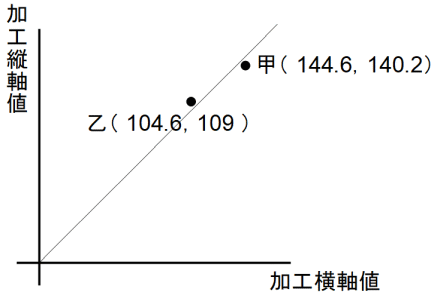
　知能ベクトルの大きさは総合的知能を表し、知能ベクトルの x 成分は数学的知能を表し、知能ベクトルの y 成分は歴史学的知能を表します。
　座標軸を原点を中心にして45°反時計回りに回転させる座標変換により、甲さんの知能ベクトル と 乙さんの知能ベクトル は次のように変換されます。
　　　
　　　　　　　　　　　
　　　　　　　　　　　
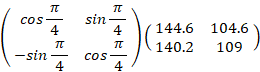
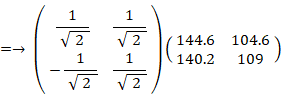
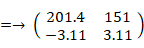
　　　甲さんの知能ベクトル ( 201.4, −3.11 )
　　　乙さんの知能ベクトル ( 151, 3.11 )

　　　　　　　　

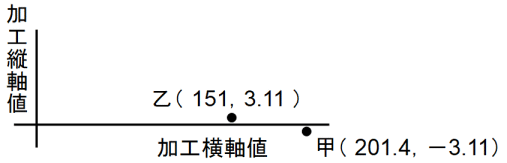
　このとき、横軸はおよそ２教科の知能の総合力を反映するものとなっており、縦軸は数学的知能と歴史学的知能とを比較してどちらが強いのかを表すものになっています。縦軸の値が正の数のときは、数学的知能よりも歴史学的知能の方が優っていることを意味しています。そしてそれは、記憶力のほうが論理的思考力よりも強いことを意味しています。

　主成分分析とは、いわば「データーの塊に１つ以上の切り口の断面をとって違いを見やすくすること」なのです。


　　　







　　

　　

　　

　　



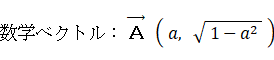
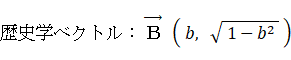
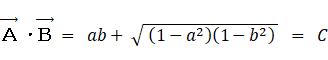
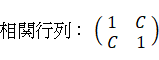
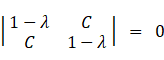
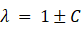
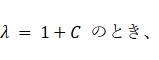
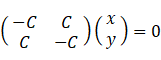
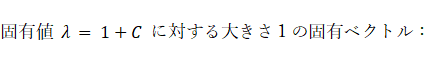
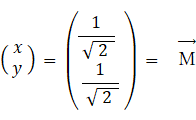
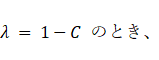
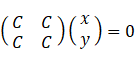
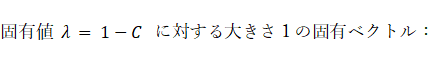
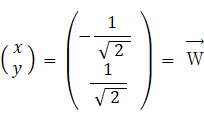
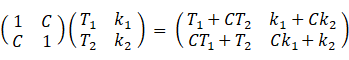
２人の知能ベクトル：
　　
　　
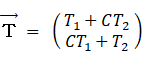
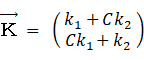
太郎の第１主成分：
　　
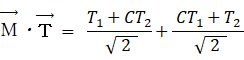
太郎の第２主成分：
　　
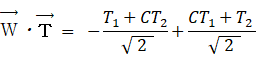
恵子の第１主成分：
　　
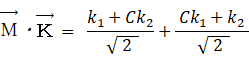
恵子の第２主成分：
　　

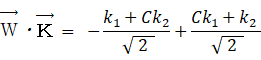
太郎の第１主成分と第２主成分：
　　
　　　　　　　　

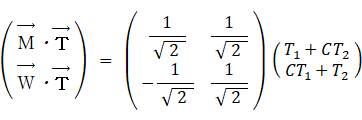
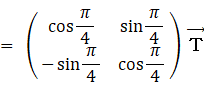
恵子の第１主成分と第２主成分：
　　
　　　　　　　　

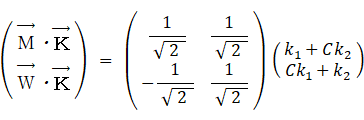
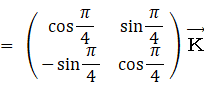
　第１主成分は総合的知能を表し、第２成分は大きいほど数学的知能よりも歴史学的知能の方が優っていることを表します。

（３）たった２人の２個ずつのデーターで主成分分析をしてみる

　数学には、論理的思考力が 67.4%、記憶力が 32.6% 必要です。歴史学には、論理的思考力が 32.6%、記憶力が 67.4% 必要です。
　　　　　　　※ 0.9 ² ＋ 0.436 ² ＝ 1
　　　　　　　※ 0.9 / ( 0.9 ＋ 0.436 ) ＝ 0.674

数学者になる素質が十分にある生徒Ａ君の数学と歴史学の年間平均点は次のようになっています。
　　（ 90.0点, 43.6点 ）
歴史学者になる素質のある生徒Ｂ君の数学と歴史学の年間平均点は次のようになっています。
　　（ 21.8 点, 45.0点 ）
２人の数学と歴史学の年間平均点の平均値は次のようになります。
　　（ 55.9点, 44.3点 ）
分散は次のようになります。
　　（ 1162.81点, 0.49点 ）
標準偏差は次のようになります。
　　（ 34.1点, 0.7点 ）
Ａ君の数学と歴史学の年間平均点の偏差比は次のようになります。
　　（ 1, −1 ）
Ｂ君の数学と歴史学の年間平均点の偏差比は次のようになります。
　　（−1, 1 ）

　　　　

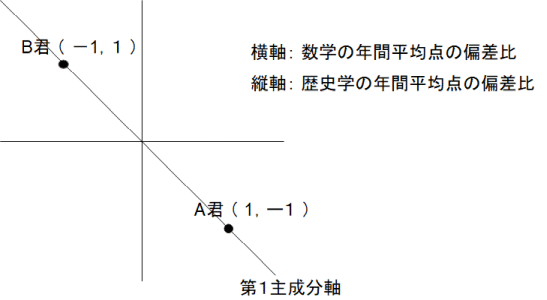
Ａ君の数学と歴史学の年間平均点の偏差比 と Ｂ君の数学と歴史学の年間平均点の偏差比 との共分散は次のようになります。
　　 −1
相関行列は次のようになります。
　　
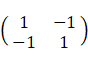
相関行列の最大固有値とそれに対応する大きさ 1 の固有ベクトルは次のようになります。
　　　固有値： 2　　　大きさ 1 の固有ベクトル： ( 0.707, −0.707 )
この固有ベクトルの方向が第１主成分の方向です。
Ａ君の数学と歴史学の年間平均点の偏差比の加工された第１主成分は次のようになります。
　　　0.707 × 1 ＋（−0.707 ）×（ −1 ） ＝→　1.414
Ｂ君の数学と歴史学の年間平均点の偏差比の加工された第１主成分は次のようになります。
　　　0.707 ×（ −1 ）＋（−0.707 ）× 1　＝→　−1.414
第１主成分は、論理的思考力 と 記憶力 との比率から数学的素質が大きいか歴史学的素質が大きいのかを見ています。

相関行列の最小固有値とそれに対応する大きさ 1 の固有ベクトルは次のようになります。
　　　固有値： 0　　　大きさ 1 の固有ベクトル： ( 0.707, 0.707 )
この固有ベクトルの方向が第２主成分の方向です。第２主成分の方向は第１主成分の方向に対して垂直です。
Ａ君の数学と歴史学の年間平均点の偏差比の加工された第２主成分は次のようになります。
　　　0.707 × 1 ＋ 0.707 ×（ −1 ） ＝→　0
Ｂ君の数学と歴史学の年間平均点の偏差比の加工された第２主成分は次のようになります。
　　　0.707 ×（ −1 ）＋ 0.707 × 1　＝→　0

Ａ君の数学と歴史学の年間平均点の偏差比の加工された第１主成分と第２主成分は次のようになります。
　　（ 1.414, 0 ）
Ｂ君の数学と歴史学の年間平均点の偏差比の加工された第１主成分と第２主成分は次のようになります。
　　（ −1.414, 0 ）