演算テンソルの表現行列が対称行列である場合、 2つの固有ベクトルは直交するので、 大きさ 1 の固有ベクトルが基底となる固有ベクトル空間への座標変換テンソルは等長変換となるため、 その表現行列は直交行列になります。
< 演算テンソルの固有ベクトル空間への変換 >
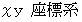 において、
において、 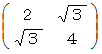 という表現行列を持つ演算テンソルによる 曲線A から 曲線B への写像は、 次のようになります。
という表現行列を持つ演算テンソルによる 曲線A から 曲線B への写像は、 次のようになります。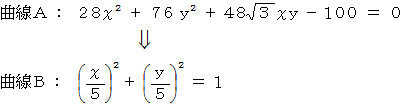
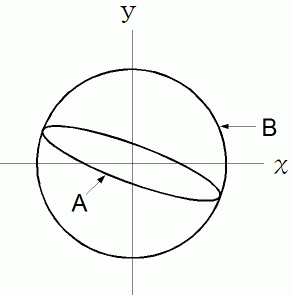
これを、
 で見ると、
で見ると、 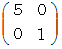 という表現行列を持つ演算テンソルによる 曲線A から 曲線B への写像になります。
という表現行列を持つ演算テンソルによる 曲線A から 曲線B への写像になります。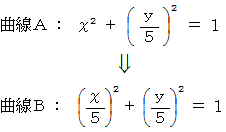
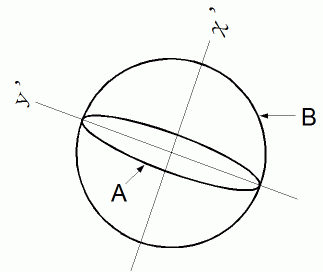
 ( 固有ベクトル空間 ) では、 この写像は、 曲線A上の点の
( 固有ベクトル空間 ) では、 この写像は、 曲線A上の点の  座標値のみを5倍にするという変換であり、
座標値のみを5倍にするという変換であり、 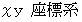 で見るよりもずっと解りやすいと思います。 対称行列を表現行列とする演算テンソルにとっては、
で見るよりもずっと解りやすいと思います。 対称行列を表現行列とする演算テンソルにとっては、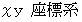 から
から  ( 固有ベクトル空間 ) への座標変換をしてくれるのは直交行列を表現行列とする座標変換テンソルになります。一般に、演算テンソルは固有ベクトル空間では対角行列を表現行列とする演算テンソルに変換されますので、 これを行列の変換にスポットを当て 「 直交行列による対称行列の対角化 」 と言います。
( 固有ベクトル空間 ) への座標変換をしてくれるのは直交行列を表現行列とする座標変換テンソルになります。一般に、演算テンソルは固有ベクトル空間では対角行列を表現行列とする演算テンソルに変換されますので、 これを行列の変換にスポットを当て 「 直交行列による対称行列の対角化 」 と言います。ではこれから、
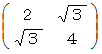 という表現行列を持つ演算テンソルを固有ベクトル空間へ座標変換してみましょう。
という表現行列を持つ演算テンソルを固有ベクトル空間へ座標変換してみましょう。演算テンソル
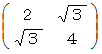 の固有値を
の固有値を 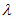 としますと、
としますと、 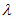 が存在する必要十分条件は、
が存在する必要十分条件は、 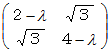 の行列式が
の行列式が  になることですから、 次のようになります。
になることですから、 次のようになります。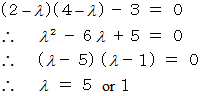
 のとき、 次の式が成り立ちます。
のとき、 次の式が成り立ちます。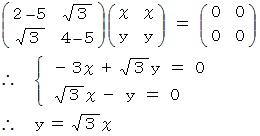
したがって、 固有ベクトルは次のようになります。
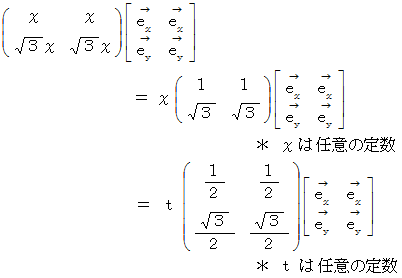
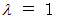 のとき、 次の式が成り立ちます。
のとき、 次の式が成り立ちます。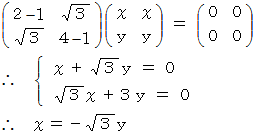
したがって、 固有ベクトルは次のようになります。
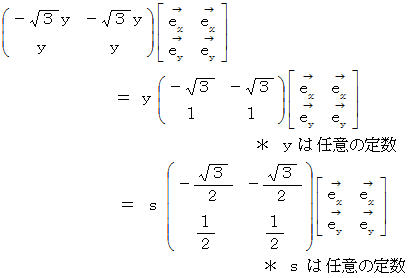
この2つの大きさが1の固有ベクトルのベクペアの表現行列は次のようになります。
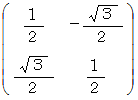
この行列は演算テンソル
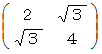 の対角化行列と言われます。 対角化行列の逆行列を表現行列とするテンソルは、演算テンソル
の対角化行列と言われます。 対角化行列の逆行列を表現行列とするテンソルは、演算テンソル 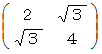 における固有ベクトル空間への座標変換テンソルです。
における固有ベクトル空間への座標変換テンソルです。対角化行列
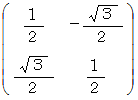 は、演算テンソル
は、演算テンソル 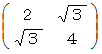 が対称行列であるため、直交行列になっています。
が対称行列であるため、直交行列になっています。演算テンソル
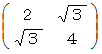 は、次のような変換式により、固有ベクトル空間では対角行列を表現行列とするものになります。
は、次のような変換式により、固有ベクトル空間では対角行列を表現行列とするものになります。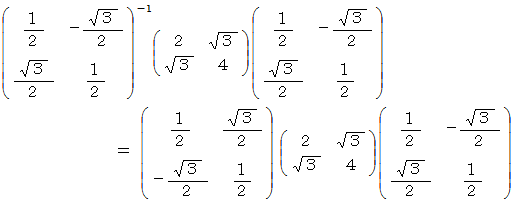
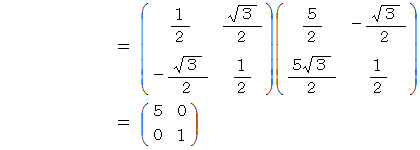
対称行列を入力すると対角化して対角化行列を表示してくれるプログラムを 十進BASIC で作ってみました。
【 備 考 】
-
元のベクトル空間での写像:

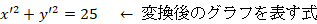
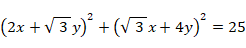

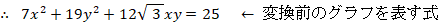

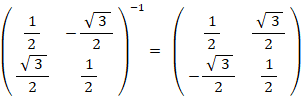
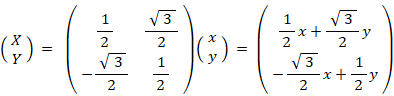
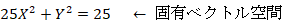
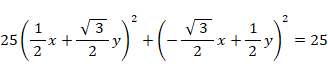

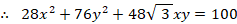
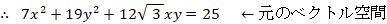
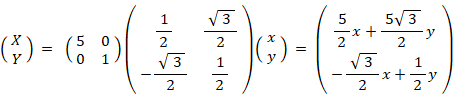
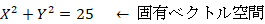
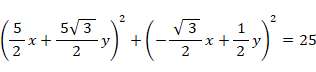

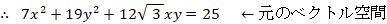
 線形代数学 へ戻る
線形代数学 へ戻る