（１） 地上（ 平坦とする ） または海上の最短コース

　 北緯45度、東経０度 の地点から、 北緯45度、東経180度 の地点に移動します。　 ずっと東に向かって地上または海上を移動した場合の移動距離　は　 北極点を通って地上または海上を最短距離で移動したときの移動距離　に対して何倍になっているでしょうか？　ただし、 地球を半径 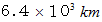の正球体とします。

（ 解 答 ）
　　　　　
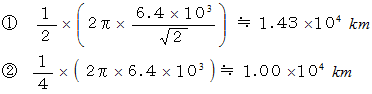
　　　　　　　　　　　　　　　　　　したがって、 答えは　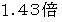　です。

（２） 大圏距離の求め方

地球上の２点間の大圏距離の求め方のガイドラインは、次のようなものです。
　　　　地球の中心と地上または海上の２点を頂点とする三角形を作ります。
　　　　地球の中心を頂点とする角の角度（ 中心角と言うことにします ）を求めます。
　　　　単位中心角あたりの大圏距離を求めます。
　　　　答えを求めます。

　 地球の中心を原点とし、 東経０度、北緯０度 の地点が 軸上になるようにし、 東経90度、北緯０度 の地点が 軸上になるようにし、 北極点が 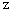軸上になるようにし、 １目盛が地球の半径になるようにして、 直交３次元座標を設定します。 すると、 東経Ｅ度、北緯Ｎ度 の地点の位置ベクトルは次のようになります。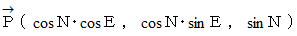
　　　　　
　 到着点の位置ベクトルから出発点の位置ベクトルを引くと、 到着点の出発点に対する位置ベクトルになります。 そのベクトル大きさから、 余弦定理を使って、 出発点と地球の中心と到着点で作られる角の大きさが解ります。

　 出発点と到着点の緯度経度を入力するとその間の大圏距離を出力するプログラムを、 十進BASIC で作ってみました。



　　　JavaScript のプログラム：
　　　出発点の東経（西経はマイナスで）  
　　　出発点の北緯（南緯はマイナスで）  
　　　到着点の東経（西経はマイナスで）  
　　　到着点の北緯（南緯はマイナスで）  

　　　  　　　大圏距離 ：   ｋｍ

（３） 大圏距離よりも短い最短コース

　 大圏距離は２点を結ぶ曲線の長さですから、 それよりも短い最短コースがあります。 それは２点間を直線で結ぶコースです。 ですから、 東京からパリまで最短距離で行こうとするならば、 トンネルを掘らなければなりません。 地球の裏側までの距離は、 大圏距離にするとちょうど 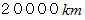ですが、 最短距離 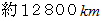に比べると随分長くなっています。