ばいおりんの慣性系相対性理論

　　等速直線運動中の列車の最後部から最前部に向けて放たれた光の到達時間についてですが、それは、車内で座っている乗客Ａにとってと線路際で座っている観察者Ｂにとってとで異なります。つまり、後者の方が若干長くなっています。それは、光の速さが一定だからです。アインシュタイン以前には、時間が絶対的で光の速さが相対的でしたが、彼がその概念を逆にしてしまったのです。光の速さが一定だから、観察者によって時間の長さが異なるわけです。観察者Ｂの慣性系の時間よりも乗客Ａの慣性系の時間のほうが短いということは、乗客Ａの方がゆっくりと活動しており、これがずっと続いた場合には乗客Ａが年齢を重ねるのが遅れるということになります。いわゆるウラシマ効果です。

　　等速直線運動中の列車の長さについてですが、それは、車内で座っている乗客Ａにとってと線路際で座っている観察者Ｂにとってとで異なります。つまり、後者の方が若干短くなっています。それは、光の速さが一定だからです。アインシュタイン以前には、空間が絶対的で光の速さが相対的でしたが、彼がその概念を逆にしてしまったのです。光の速さが一定だから、観察者によって空間の長さが異なるわけです。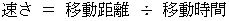

　　　　　

　では２つの慣性系で空間の長さは等しいことが暗黙の了解になっており、では２つの慣性系で時間の長さは等しいことが暗黙の了解になっています。つまり、では、「２つの慣性系で空間の長さが等しいと仮定すると、観察者Ｂの慣性系の時間よりも乗客Ａの慣性系の時間のほうが短い。」と言っていて、では、「２つの慣性系で時間の長さが等しいと仮定すると、観察者Ｂの慣性系の空間よりも乗客Ａの慣性系の空間のほうが短い。」と言っているのです。
　では、乗客Ａの慣性系の空間は縮んでいませんので、観察者Ｂにとっての光の軌道の長さは乗客Ａにとっての光の軌道の長さよりも長くなっています。「２つの慣性系で光の速さは等しい」わけですから、時間は乗客Ａの慣性系での方が長くなければならないことになります。では、乗客Ａの慣性系の時間は縮んでいませんので、観察者Ｂにとっての光の届く時間の長さは乗客Ａにとっての光の届く時間の長さよりも長くなっています。「２つの慣性系で光の速さは等しい」わけですから、空間は観察者Ｂの慣性系での方が長くなっていなければならないことになります。

　　　　　　観察者Ｂにとっての観察者Ｂに対する光の速さ
　　　　　　観察者Ｂにとっての乗客Ａに対する光の速さ
　　　　　　乗客Ａにとっての乗客Ａに対する光の速さ
　　　　　　乗客Ａにとっての観察者Ｂに対する光の速さ
　　　　　　観察者Ｂにとっての観察者Ｂに対する乗客Ａの速さ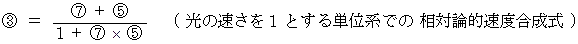

　　　　　

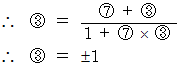
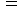
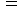
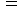
　以上のように、相対性理論が言っていることはではなくて、です。そして、移動しているものどうしの衝突については、ニュートンの教え通りを用いなければならないのです。そして、その結果は相対論的には真実ではないと付け加えておくだけで、それ以上この矛盾について詮索する必要はないのです。そうすると、相対性理論が相対性理論でなくなってしまうと思われるかもしれませんが、それでも相対性理論は電磁気学や質量の概念についてすばらしい理論を持ち続けているのです。を用いてしまうと、「やこそ、特殊相対性理論が導き出す重大な結論である。」と思ってしまうのです。まず、やの言っている意味が理解できるようになること、それは相対性理論入門です。その次に、次第にやが間違いであることに気づいていきながら、もっと奥にある真実を発見していく過程こそ相対性理論の体得だと思います。

　さて、私の四方八方からいろんな速さ（マイナスも含む）でたくさんの光源が向かって来ています。それらはある時刻に自分から同じ距離だけ離れた場所に存在するものとします。その時刻にたくさんの光源から放たれた光は、同時刻に私に届きます。これが相対性理論の基本的原理である「光速不変の原理」です。
　この光景を私に対して等速直線運動をしているあなたが見た場合、たくさんの光源から放たれた光は、同時刻に私に届くのではありません。しかし、実際には私にはすべての光が同時刻に届いているわけです。ここの所の矛盾を解決するために、定説の特殊相対性理論は「同時刻性は消失し、移動している物質は運動方向に収縮し、ゆっくりと活動する。」というのが真実であるとします。しかし、私はここの所の矛盾を解決するために、「あなたによる第３者的なニュートン力学的な観察では、光は同時刻に私に届いてはおらず、あなたの観察は幻想でしかありません。そんな幻想的観察は博物館入りにして、私の立場に立ってあなたが私のことを相対論的に観察してくれれば、すべての光が同時刻に届いているという真実に気づくはずです。」と言います。