数学と物理学 へ戻る赤玉と白玉が２個ずつ入った 袋Ｘ と 袋Ｙ と 袋Ｚ があります。
袋Ｘ から１個の玉を取り出した後に元に戻して再び１個の玉を取り出したときに、 １回目に取り出した玉の色と２回目に取り出した玉の色が異なる確率をＡ とします。
袋Ｘ から２個の玉を取り出したときに色が異なる確率をＢ とします。
袋Ｙ から１個の玉を取り出し、 袋Ｚ から１個の玉を取り出したときに、 玉の色が異なる確率をＣ とします。
確率Ａ の原始的な求め方 （ すべての組み合わせを書き出す方法 ）
|
赤１ 赤１ |
赤１ 赤２ |
赤１ 白１ |
赤１ 白２ |
|
赤２ 赤１ |
赤２ 赤２ |
赤２ 白１ |
赤２ 白２ |
|
白１ 赤１ |
白１ 赤２ |
白１ 白１ |
白１ 白２ |
|
白２ 赤１ |
白２ 赤２ |
白２ 白１ |
白２ 白２ |
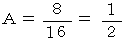
確率Ｂ の原始的な求め方 （ すべての組み合わせを書き出す方法 ）
|
|
赤１ 赤２ |
赤１ 白１ |
赤１ 白２ |
|
赤２ 赤１ |
|
赤２ 白１ |
赤２ 白２ |
|
白１ 赤１ |
白１ 赤２ |
|
白１ 白２ |
|
白２ 赤１ |
白２ 赤２ |
白２ 白１ |
|
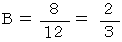
確率Ｃ の原始的な求め方 （ すべての組み合わせを書き出す方法 ）
|
Ｙ赤１ Ｚ赤１ |
Ｙ赤１ Ｚ赤２ |
Ｙ赤１ Ｚ白１ |
Ｙ赤１ Ｚ白２ |
|
Ｙ赤２ Ｚ赤１ |
Ｙ赤２ Ｚ赤２ |
Ｙ赤２ Ｚ白１ |
Ｙ赤２ Ｚ白２ |
|
Ｙ白１ Ｚ赤１ |
Ｙ白１ Ｚ赤２ |
Ｙ白１ Ｚ白１ |
Ｙ白１ Ｚ白２ |
|
Ｙ白２ Ｚ赤１ |
Ｙ白２ Ｚ赤２ |
Ｙ白２ Ｚ白１ |
Ｙ白２ Ｚ白２ |
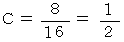
確率Ａ を原始的でない方法で求めてみます。
確率Ｂ は、 袋Ｘ から１個の玉を取り出した後に元に戻さずに再び１個の玉を取り出したときに、 １回目に取り出した玉の色と２回目に取り出した玉の色が異なる確率と同じです。 原始的でない方法で確率Ｂ を求めてみます。
確率Ｃ を原始的でない方法で求めてみます。
確率Ａ と 確率Ｃ は、 確率論的には同じ行為ですので、 確率Ａ と 確率Ｂ とを比べてみましょう。 確率Ａ は、 同じ行為を２回繰り返して行っており、 １回目の行為が２回目の行為に影響を及ぼすことはありません。 これに対して確率Ｂ は、 １回目の行為が２回目の行為に影響を及ぼしています。 この違いは、 古典力学的観察 と 量子力学的観察 との違いに似ています。
※ 参照： 大学生のための数学 ＞ 確率 ＞ 同時を異時とみなす確率問題