十進分子が １ である正の分数のことを 単位分数 といいます。
ある自然数を複数の単位分数の和で表すことを 単位分数分解 と言います。
今回は １ を単位分数分解してみましょう。 ただし、 最小の単位分数を
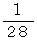とし、 すべて異なる単位分数を用いるものとします。
古典的方法まず、 完全数 （ すべての約数の和が自分自身に等しい自然数 ） を使って単位分数分解を行います。
６ ＝ １＋２＋３
２８ ＝ １＋２＋４＋７＋１４
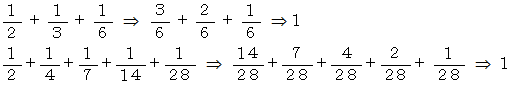
次に、 次の等式を用いて広げてきます。
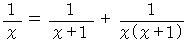
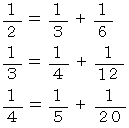
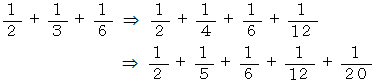
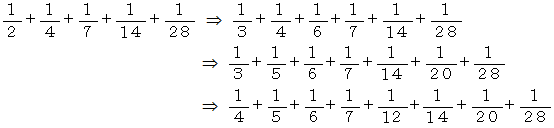
以上の方法で ７通りの １ の単位分数分解 （ 条件付き ） を見つけることができました。 しかし、 実際にはまだまだあります。 すべてを求めるためには、 コンピューターの力を借りたほうがよさそうです。
十進BASIC のプログラムを作って探し出す方法山中和義 / 電脳遊戯団 さんがネット上に公開されているプログラム集の中に次のようなものがあります。（ 一部変更しています。） これを用いると、 答えがたくさんあることが解ります。
OPTION ARITHMETIC RATIONAL ! 有理数モード
PUBLIC NUMERIC N ! 上限
LET N = 28
DIM F(N), A(N), B(N)
MAT F = ZER
PRINT "＜ １の単位分数分解 ＞"
LET A(N) = 1/N
LET B(N) = A(N)
FOR i = N−1 TO 1 STEP -1
LET A( i ) = 1/i
LET B( i ) = A( i ) + B( i + 1 )
NEXT i
CALL try ( 1, 1, A, B, F )
END
EXTERNAL SUB try ( M, P, A( ), B( ),F( ) )
OPTION ARITHMETIC RATIONAL
FOR i = P TO N
LET T = M−A( i )
IF T = 0 THEN
FOR j = 1 TO P-1
IF F( j ) = 1 THEN
PRINT " 1/ " ; STR$( j ) ; " + ";
END IF
NEXT j
PRINT " 1/ " ; STR$( i )
ENDIF T > 0 AND i < N THEN
IF B( i + 1 ) < T THEN EXIT FOR
LET F( i ) = 1
CALL try ( T, i + 1, A, B, F )
LET F( i ) = 0
END IF
NEXT i
END SUB
わかりやすくするために、 最小の単位分数を
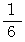として、 つまり、 このプログラムの N = 28 を N = 6 に書き換えて、 このプログラムのアルゴリズムを見てみましょう。まず、 次のような数を作っています。
A(1) = 1/1
A(2) = 1/2
A(3) = 1/3
A(4) = 1/4
A(5) = 1/5
A(6) = 1/6
B(1) = 1/1 + 1/2 + 1/3 + 1/4 + 1/5 +1/6 = 49/20
B(2) = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 = 29/20
B(3) = 1/3 + 1/4 + 1/5 + 1/6 = 19/20
B(4) = 1/4 + 1/5 + 1/6 = 37/60
B(5) = 1/5 + 1/6 = 11/30
B(6) = 1/6
F(n) = 0
そして、 後は、 これらの数たちを扱う関数 Try ( 1, 1, A, B, F ) を用いて、 答えを画面に出力して終わりです。
では、 この関数のアルゴリズムがどうなっているのか見ていきましょう。
まず、 １ が A(1) に等しくなっているかどうかを見ます。 すると等しくなっています。 したがって、 １ はA(1) という１つの単位分数で表されることがわかります。 これを画面に出力します。
次に、 １ が A(2) に等しくなっているかどうかを見ます。 もちろん等しいはずがありません。 なぜなら A(1) > A(2) だからです。 その次に、 １ から A(2) を取り除いたものが B(3) に等しくなっているかどうかを見ます。 もし等しいのであれば、 画面に 1/2 + 1/3 + 1/4 + 1/5 + 1/6 と出力すれば答えの１つを表現することができます。しかし実際は、 １ から A(2) を取り除いたものは B(3) に等しくなってはいません。 次に、 １ から A(2) を取り除いたものが、 B(3) のある部分 に等しくなっている可能性があるかどうか見ます。 それには B(3) が １ から A(2) を取り除いたものより小さくはないことを確認すればいいのです。 その結果、 その可能性があることがわかります。
そこで次に、 １ から A(2) と A(3) を取り除いたものが B(4) に等しくなっているかどうかを見ます。 すると等しくはありません。 そこで次に、 １ から A(2) と A(3) を取り除いたものが、 B(4) のある部分 に等しくなっている可能性があるのかどうかを見ます。 その結果その可能性がないことが解りますので、 今度は、 １ から A(2) と A(3) を取り除いたものが B(5) に等しくなっているかどうかを見ます。 すると等しくはありません。 そこで次に、 １ からA(2) と A(3) を取り除いたものが、 B(5) のある部分 に等しくなっている可能性があるのかどうかを見ます。 これも可能性がありませんので、 次は、 １ からA(2) と A(3) を取り除いたものがB(6) に等しくなっているかどうかを見ます。 すると等しくなっていますので、 画面に 1/2 + 1/3 + 1/6 と出力して、 答えの１つを表現します。
次に、 １ から A(2) と A(4) を取り除いたものが B(5) に等しくなっているかどうかを見ます。 すると等しくはありません。 そこで次に、 １ から A(2) と A(4) を取り除いたものが、 B(5) のある部分 に等しくなっている可能性があるのかどうかを見ます。 その結果その可能性があることが解りますので、 今度は、 １ から A(2) と A(4) と A(5) を取り除いたものが B(6) に等しくなっているかどうかを見ます。 すると等しくはありません。
次に、 １ から A(2) と A(5) を取り除いたものが B(6) に等しくなっているかどうかを見ます。 すると等しくはありません。
次に、 １ から A(3) を取り除いたものが B(4) に等しくなっているかどうか見ます。 その結果、 等しくなっていませんので、 その次に、 １ から A(3) を取り除いたものが、 B(4) のある部分 に等しくなっている可能性があるかどうか見ます。 するとその可能性がないことがわかります。 この後は、 B(5) 、 B(6) とさらに進めていっても、 その可能性はさらに遠のいていきますし、 １ から A(4) を取り除いたものを考えても、 その可能性はさらに遠のいていきますので、 この時点でこの関数の処理を終了することにします。
以上のような N = 6 のときの呼び出し関数 Try(1,1,A,B,F) の具体的な処理手順は、 次のようになっています。
Try ( 1, 1, A, B, F ) の処理を開始する。
i = 1
T = 1−A(1) = 0
PRINT “1/1” 改行する。
i = 2
T = 1−A(2) = 1/2 > 0
B(3) > 1/2
F(2) = 1
再ＣＡＬＬ Try ( 1/2, 3, A, B, F)
i = 3
T = 1/2−A(3) = 1/2−1/3 = 1/6 > 0
B(4) > 1/6
F(3) = 1
再再ＣＡＬＬ Try(1/6,4,A,B,F)
i = 4
T = 1/6−A(4) = 1/6−1/4 < 0
i = 5
T = 1/6−A(5) = 1/6−1/5 < 0
i = 6
T = 1/6−A(6) = 1/6−1/6 = 0
PRINT “ 1/2 + ” 改行せず。
PRINT “1/3 + ” 改行せず。
PRINT “1 /6 ” 改行する。
再再ＣＡＬＬ終了
F(3) = 0
i = 4
T = 1/2−A(4) = 1/2−1/4 = 1/4 > 0
B(5) > 1/4
F(4) = 1
再再ＣＡＬＬ Try ( 1/4, 5, A, B, F )
i = 5
T = 1/4−A(5) = 1/4−1/5 = 1/20 > 0
B(6) > 1/20
F(5) = 1
再再再ＣＡＬＬ Try ( 1/20, 6, A, B, F )
i = 6
T = 1/20−1/6 < 0
再再再ＣＡＬＬ終了
F(5) = 0
i = 6
なにもせず
再再ＣＡＬＬ終了
F(4) = 0
i = 5
T = 1/2−A(5) = 1/2−1/5 = 3/10 > 0
B(6) < 3/10
再ＣＡＬＬ中断
F(2) = 0
i = 3
T = 1−A(3) = 2/3
B(4) < 2/3
Try ( 1, 1, A, B, F ) の処理を中断して終了する。
＜ コピペ用の小窓 ＞