(1) 物理量単位 と 非物理量単位
-
物理量単位の代表は「
 」であり、 非物理量単位の代表は「 個 」です。 物理量単位は具体的であり、 非物理量単位は、 円 や ラジアン を除いて一般に抽象的です。 物理量単位は具体的なものですから、 物理学では単位を含んだ等式が用いられます。 このとき、 非物理量単位は「 無単位 」であり「 無次元 」であるとみなされます。
」であり、 非物理量単位の代表は「 個 」です。 物理量単位は具体的であり、 非物理量単位は、 円 や ラジアン を除いて一般に抽象的です。 物理量単位は具体的なものですから、 物理学では単位を含んだ等式が用いられます。 このとき、 非物理量単位は「 無単位 」であり「 無次元 」であるとみなされます。「 4人のお友達が、 それぞれビー玉を10個ずつ持っています。 ビー玉は全部で何個あるでしょうか?」 この答えを導き出すための式は、 数学の式を使います。

この数学の式を解説すると、 次のようになります。
「 10個を4倍すると、 40個になる。 この問題においては、 人は単位ではない。」
「
 の大きさの重力場が存在する点に質量
の大きさの重力場が存在する点に質量  の物質が存在するとき、 この物質に作用する重力の大きさを求めなさい。」 この答えを導き出すためには、 物理学の式を使います。
の物質が存在するとき、 この物質に作用する重力の大きさを求めなさい。」 この答えを導き出すためには、 物理学の式を使います。
この物理学の式を解説すると次のようになります。
「 質量
 に
に  の大きさの重力場をかけるという演算をすると、
の大きさの重力場をかけるという演算をすると、  の大きさの力 が得られる。 物理学では式の意味を大切にする。」
の大きさの力 が得られる。 物理学では式の意味を大切にする。」「 質量
 の物質に
の物質に  の力を加え続けると、 その物質はどれくらいの大きさの加速度で移動するでしょうか?」 この答えを導き出すためには、 物理学の式を使います。
の力を加え続けると、 その物質はどれくらいの大きさの加速度で移動するでしょうか?」 この答えを導き出すためには、 物理学の式を使います。
この物理学の式を解説すると次のようになります。
「
 という変位のしやすさを表す物理量に、
という変位のしやすさを表す物理量に、  の大きさの力をかけるという演算をすると、
の大きさの力をかけるという演算をすると、  の大きさの加速度 が得られる。」
の大きさの加速度 が得られる。」物理学の式には、 必ず単位が含まれます。 その例を3つ挙げます。
 同質単位変換
同質単位変換
 速さ : 変位( 移動空間 )を 経過( 移動時間 )で割る
速さ : 変位( 移動空間 )を 経過( 移動時間 )で割る
 エネルギー( 仕事 ): 力を変位で積分する( 次の例は力が一定の場合 )
エネルギー( 仕事 ): 力を変位で積分する( 次の例は力が一定の場合 )
角度の単位は非物理量単位ですが、 具体的です。 角度の単位は、 物理量単位に近いので、 補助単位と言われます。 扇形の中心角は、 弧の長さの半径に対する比率で表されます( 弧度法 )。 角度の単位は無次元です。 たとえば、 角速度の単位は
 ですが、 角速度の次元は
ですが、 角速度の次元は  です。
です。 単位系 と 次元
単位系 と 次元-
物理学の国際単位系は、
 単位系 と言われます。 これは、 長さ
単位系 と言われます。 これは、 長さ  、 質量
、 質量  、 時間
、 時間 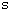 、 電流
、 電流  、 温度
、 温度 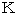 、 物質量
、 物質量  、 光度
、 光度  を基本単位とします。 これらの基本単位や補助単位を組み合わせて、 組立単位( ロゴなし )や 組立単位( ロゴあり )が作られます。
を基本単位とします。 これらの基本単位や補助単位を組み合わせて、 組立単位( ロゴなし )や 組立単位( ロゴあり )が作られます。組立単位( ロゴなし )の例 :
速度

加速度

角速度

組立単位( ロゴあり )の例 :
力

エネルギー

電気量

次元 とは、 補助単位を無次元としたときの、 組立単位を構成している基本単位のことです。 基本単位の ・ ・ ・ −2乗、 −1乗、 1乗、 2乗 ・ ・ ・ は、 それぞれ異なる次元になります。
物理学の公式は、 次の
 のように次元を含む等式で表すような習慣をつけておくと、「 次元解析 」という手法によって、 いろんなものが見えてくるようになります。 その例を2つ挙げてみます。
のように次元を含む等式で表すような習慣をつけておくと、「 次元解析 」という手法によって、 いろんなものが見えてくるようになります。 その例を2つ挙げてみます。例1: 運動方程式





以上のような手順で
 に到着するのですが、 逆に、 力の単位を
に到着するのですが、 逆に、 力の単位を  の右辺のように2つに分解して、「 力とは、 質量に加速度をかけたものである。」または「 力とは、 質量を加速度で積分したものである。」という法則が存在しているのではないか、と予想することができます。
の右辺のように2つに分解して、「 力とは、 質量に加速度をかけたものである。」または「 力とは、 質量を加速度で積分したものである。」という法則が存在しているのではないか、と予想することができます。例2 : ローレンツ力
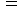 クーロン力
クーロン力 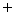 狭義の意味でのローレンツ力
狭義の意味でのローレンツ力( 4次元への拡張 )
( 電流
 の代わりに電荷量
の代わりに電荷量 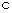 を基本単位にしています。
を基本単位にしています。  )
) クーロン力の大きさを表す式
クーロン力の大きさを表す式
 狭義の意味でのローレンツ力の大きさを表す式
狭義の意味でのローレンツ力の大きさを表す式
クーロン力の定数 と 狭義の意味でのローレンツ力の定数 とを比べてみましょう。 つまり、
 と
と  とをです。 この2つの違いは、 クーロン力の定数の方には
とをです。 この2つの違いは、 クーロン力の定数の方には  がついていることと、 クーロン力の定数の次元の方が、
がついていることと、 クーロン力の定数の次元の方が、  だけ多いということです。 ここで、
だけ多いということです。 ここで、  とは光の速さであることを確認してください。 すると、 次のような疑問というか仮定が浮かんできます。
とは光の速さであることを確認してください。 すると、 次のような疑問というか仮定が浮かんできます。
クーロン力の式に含まれる
 は、 本当は、 単なる
は、 本当は、 単なる  ではなくて、
ではなくて、  ではないか? とすると、 クーロン力の大きさは、 本当は次の式で表されるのではないか?
ではないか? とすると、 クーロン力の大きさは、 本当は次の式で表されるのではないか?
こう考えると、 クーロン力 と 狭義の意味でのローレンツ力 とが統一され、 数学的にきれいなローレンツ力の定義式になります。 また、 相対性理論で登場する「 4次元電流 」とも繋がります。
 基礎物理学 へ戻る
基礎物理学 へ戻る