質量 0.1 kg の物質の自然落下について考えます。
落下開始地点から落下方向への距離を r m とします。
落下開始時点の物質の運動エネルギーや運動量は０です。
落下開始後 t s まで物質には落下方向へ 0.1 g N の力が作用し続けます。

時刻 t s における運動方程式：
　　　
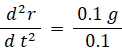
両辺を t で積分して、
　　　
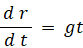
両辺をさらに t で積分して、
　　　

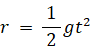
したがって、運動エネルギー(E) と 運動量(P) について次の式たちが成り立つ。
　　　
　　　

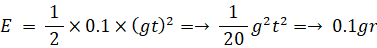
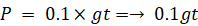
したがって、運動エネルギー(E) と 運動量(P) について次のことが言えます。（ 力が一定の場合 ）
　　　運動エネルギーの変化 ＝ 力・変位　　（ 内積で、結果はスカラー ）
　　　運動量の変化 ＝ 力 × 時間　　（ ベクトル 外積ではありません ）

　　　　　　　　　　　※　スカラーに属するもの： 時間　運動エネルギー　距離
　　　　　　　　　　　※　ベクトルに属するもの： 変位　力　運動量

　力が一定の場合、 力・変位（ 内積 ）は 仕事 を表し、 力 × 時間 は 力積 を表します。

　力が一定の場合、仕事は、始点から終点までの経路に関わらず、力・変位（ 内積 ）で表されます。