(1) 予習
-
問題1:
底辺と高さの長さの等しい三角形で、 3つの辺の長さの和が最小の三角形は、 二等辺三角形であることを証明してください。
( 証明 )
二等辺三角形の底辺を形成している線分を
 とする。
とする。点
 と 点
と 点 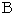 を焦点とし、 二等辺三角形の頂点
を焦点とし、 二等辺三角形の頂点  を通る楕円を描く。
を通る楕円を描く。点
 を通り、線分
を通り、線分 に平行な直線を描く。
に平行な直線を描く。その直線上の任意の点を
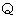 とする。
とする。線分
 と楕円の交点を
と楕円の交点を  とする。
とする。このとき、 次の式たちが成り立っている。

したがって、 次の式が成り立つ。


問題2:
-
サッカーコートを思い浮かべてください。 ハーフウェイライン
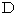 を境に、 上側コートにスタートポイント
を境に、 上側コートにスタートポイント 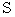 を作り、 下側コートにゴールポイント
を作り、 下側コートにゴールポイント 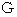 を作ります。 移動の条件が与えられた時に、
を作ります。 移動の条件が与えられた時に、 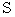 から
から 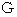 へ最短時間で移動できるコースについて考えてみましょう。 移動の条件は、 上側コート内では速さ
へ最短時間で移動できるコースについて考えてみましょう。 移動の条件は、 上側コート内では速さ  で、 下側コート内では、 速さ
で、 下側コート内では、 速さ  であるということです。 曲がっていようが折れていようがどんなコースをとってもかまいませんが、 最短時間でゴールできるコースを考えてください。
であるということです。 曲がっていようが折れていようがどんなコースをとってもかまいませんが、 最短時間でゴールできるコースを考えてください。
-
中心
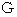 半径
半径 の円の中からはみ出るようなコースを考える人はまずいないと思います。 また、 曲線のコースを考える人はいないと思います。 それは、 曲がっていない平面上では2点を結ぶ最短の線分は直線だからです。 結局、 線分
の円の中からはみ出るようなコースを考える人はまずいないと思います。 また、 曲線のコースを考える人はいないと思います。 それは、 曲がっていない平面上では2点を結ぶ最短の線分は直線だからです。 結局、 線分 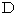 上の点
上の点  を経由するコースが最短になります。 イメージですから、 図は少々の誤差があります。
を経由するコースが最短になります。 イメージですから、 図は少々の誤差があります。
-
光 ( 電磁波 ) の現象には、 次のようなものがあります。
吸収 透過 反射 屈折 干渉 分光 偏光 回折 散乱
プリズムによる分光については、「 波長の短い光ほど屈折率が大きい。」という法則があります。 これは、「 光の最短時間伝播経路の法則 」に由来します。 真空中を伝わる光の速さは、 光の波長に関係なく一定ですが、 ガラスや水の中を伝わるときには、 波長の短い光( 振動数の大きい光 )ほど遅くなります。 そこで 「 光の最短時間伝播経路の法則 」 により、 波長の短い光ほど屈折率が大きくなるというわけです。 予習のサッカーコートでいうと、 点
 が 点
が 点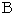 に近づいていきます。
に近づいていきます。さて、 振幅や振動数が等しくて、 位相の異なる2つの波があります。

 は
は  よりも 位相が
よりも 位相が  だけ進んでいます。
だけ進んでいます。  も
も  も同じ光源から放たれる光子で、 放たれる時刻が
も同じ光源から放たれる光子で、 放たれる時刻が  の方が
の方が  よりも
よりも  だけ早くて、
だけ早くて、  の光子が遠回りをして来たために、 後から放たれた
の光子が遠回りをして来たために、 後から放たれた  の光子に追いつかれてある時刻
の光子に追いつかれてある時刻  にある場所で重なったとしましょう。 この場合は、 その瞬間その場所で、 波の合成により、 次のような波の光子になります。
にある場所で重なったとしましょう。 この場合は、 その瞬間その場所で、 波の合成により、 次のような波の光子になります。
この場所では、 その次の瞬間に、
 と
と  と同様の関係をした、
と同様の関係をした、  と
と 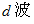 が同様のことを起こして、 次のような波の光子になります。
が同様のことを起こして、 次のような波の光子になります。
このような繰り返しで、 結局、 その2つの光子が出会う場所では、 次のような波が存在することになります。

光の速さを
 とすると、
とすると、 の時間に進む光の距離は
の時間に進む光の距離は  ですから、
ですから、  の光子ほうが
の光子ほうが  の光子よりも
の光子よりも  だけ長い道のりを通って、 ある場所で
だけ長い道のりを通って、 ある場所で  の光子に追いつかれるようなケースの場合は、 その場所では上記のような光子の波の合成が起きていることになります。
の光子に追いつかれるようなケースの場合は、 その場所では上記のような光子の波の合成が起きていることになります。さて、 この合成波において、 次のことを言うことができます。

したがって、 次のようになります。

以上から、 追いつき追いつかれて重なり合う2つの同光源からの光子の波の合成は、 合成場所の光源からの道のりの差によって形が異なることがわかります。 さらに、 その道のりの差が変化すると、 周期的に波の形は変化し、 その変化のしかたは光の振動数によって異なることもわかります。 この原理を、私は発見者の名前をとって「 ファインマンの兄弟光子合成の原理 」と言っています。 ファインマンは、 この原理をうまく活用して、 シャボン玉やCDディスクによって反射された光の干渉による構造色のしくみを解明するとともに、 光の屈折や反射を説明することのできる「 光の最短時間伝播の法則 」の根拠を解明して、 世間をあっと言わせたのです。

彼は、 まず、 光の反射は、 入射角に関係なく、 すべての反射角をとるという発想から始めます。 そして、 まず、 薄膜構造 あるいは 格子構造 の異なる2か所で反射された後に「 同一場所で初めて出会う2つの兄弟光子たちの年齢差 」によって異なる「 合成波の振幅 」が空間に形成するスカラー場をとり、 それを数個の異なる振動数の光を発生する光源を使ってみた時の不均一性が干渉模様 であることを解明しました。
次に彼は、 同一平面上の異なる場所で反射された後に「 同一場所で初めて出会って合成波を形成する無数の兄弟光子たち 」の、 相殺し合う年齢差の影響を受けずに、合成波の振幅を形成する要素になっている年齢差の非常に少ない兄弟光子たちの中で最も若い光子の経路が、 その合成された光子の経路になっており、 それは、 入射角と反射角が等しくなっていることを解明しました。

さらに彼は、 空中から来てガラスの異なる表面から内に入ってきた後に 「 同一場所で初めて出会って合成波を形成する無数の兄弟光子たち 」 の、 相殺し合う年齢差の影響を受けずに、 合成波の振幅を形成する要素になっている年齢差の非常に少ない兄弟光子たちの中で最も若い光子の経路が、 その合成された光子の経路になっており、 それは、 ガラスの表面で少し方向を変更した屈折経路になっていることを解明しました。
反射や屈折の経路は、 予習でやったように、 光子の移動の、 つまり光の伝播の最短時間コースになっています。
 量子力学 へ戻る
量子力学 へ戻る