x y 平面があります。 x 軸上を原点を中心として振幅 A (m) で単振動している質量 m (kg) の物質があります。
時刻0(s) に 物質は x=A の位置にあり、時刻 2 π / ω (s) に再び x=A の位置に戻ってきます。
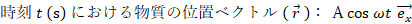
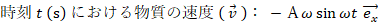
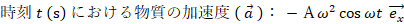
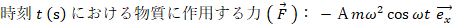
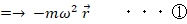
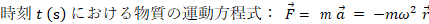
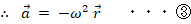
※ ③ は「単振動の運動方程式」と言われます。
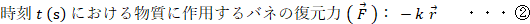
① と ② を比べて、
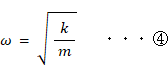
④ を ③ に代入して、
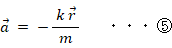
③ と ⑤ は「バネの運動方程式」と言われます。
単振動の運動方程式:
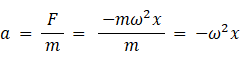
単振動の運動方程式: a = -ω2 x ・・・ ⑥
無重力でのバネの単振動の振動数: ω = root ( k / m ) ・・・ ⑦
※ k はバネ定数で、m は重りの質量
⑦ を ⑥ に代入すると、
a = -k x / m ・・・ ⑧
⑧ を見ると ⑥ が運動方程式と言われる理由が分かります。
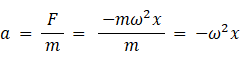
単振動の運動方程式: a = -ω2 x ・・・ ⑥
無重力でのバネの単振動の振動数: ω = root ( k / m ) ・・・ ⑦
※ k はバネ定数で、m は重りの質量
⑦ を ⑥ に代入すると、
a = -k x / m ・・・ ⑧
⑧ を見ると ⑥ が運動方程式と言われる理由が分かります。
 力学 へ戻る
力学 へ戻る