【 問 題 】

下図のような半径 10 cm の円を幅１cm ごとに10区分したものがある。
　　　　　　　　　　　　　　　　　　　　　　　　（ 中心部分は幅 ２cm ）
　　　　　　　

　（１） 黒色と灰色の部分の面積の差はいくらか？
　　 　また、 黒色の部分の面積は灰色の部分の面積の何倍か？

　（２） 次の式は、 別の方法で黒色と灰色の部分の面積の差を求めたものである。
　　　　　　　　
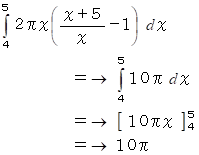
　　　　この式の意味を示しなさい。

【 解 答 】

　（１）

黒色の部分の面積 ：
　　　π10² − π９²　＝　19π cm²
　　　または、 道幅の面積 より、 ２π9.5 × １　＝　19π cm²

灰色の部分の面積 ：
　　　π５² − π４²　＝　９π cm²
　　　または、 道幅の面積 より、 ２π4.5 × １　＝　９π cm²

よって、
　　差は １０π cm²　であり、
　　黒色の部分の面積は灰色の部分の面積の　19 / ９　＝→　2.1111・・・ 倍 である。

　（２）

　 まず、 灰色の部分は中心を同じくする半径４〜５ cm の円が無数に集まっているものと考え、 灰色の部分を構成する円とそれよりも ５ cm 半径の大きい黒色の部分を構成する円とを対応させて、 その円周の長さの差を隣の円までの距離で積分して面積の差を求める。