（ 問 題 ）

　 ０ 〜 ９ の整数が書かれたカードが１枚ずつあります。 この10枚のカードから任意に３枚を選んだときに、 隣り合う数が含まれる確率はいくらになるでしょうか？

（ 解 答 ）

　 隣り合う数が含まれない場合の数を求めてから、その数をすべての場合の数から引いて、隣り合う数が含まれる場合の数を求めることにします。

選ばれなかった数たち７つを小さい順に並べます。

　　　　

その両端と間に 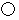を入れていきます。

　　　　

例えば、１ と ４ と ６ の３枚のカードを選んだとき、 次のようなイメージにします。

　　　　

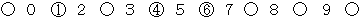
例えば、０ と ４ と ９ の３枚のカードを選んだとき、 次のようなイメージにします。
　　　　

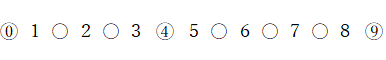
例えば、３ と ６ と ９ の３枚のカードを選んだとき、 次のようなイメージにします。
　　　　

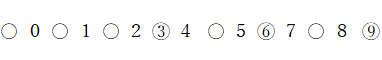
例えば、３ と ５ と ７ の３枚のカードを選んだとき、 次のようなイメージにします。
　　　　

　 このようなケースをすべて挙げていけばいいので、 隣り合う数が含まれない場合の数は、 ８個の から３個を選ぶ組み合わせの数に等しいことがわかります。 つまり、 次のようになります。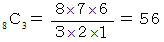
　　　　
10枚から３枚を選ぶ組み合わせの数は次のようになります。
　　　　　
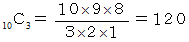
したがって、 隣り合う数が含まれる場合の数は次のようになります。
　　　　120 − 56 ＝ 64
よって、 求める確率は次のようになります。
　　　　64 ÷ 120 ≒ 53.3 ％


　 十進BASIC で次のようなプログラムを作って実行したところ、 答えが正しいことがわかりました。


　JavaScript のプログラム（ 10万回試行 ）：
　　　隣り合うカードが含まれていた割合 ：　 ％