（１） オイラーの公式を用いる証明法

　 三角関数 指数・対数関数 ＞ 余弦定理よ　で述べたように、 加法定理 は 余弦定理 を用いて証明することもできます。 一方、 オイラーの公式 と 複素数ベクトルのかけ算 を用いた証明もあります。

　　　オイラーの公式 ：
　　　　　　　　
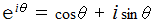
　　　複素数ベクトルのかけ算 ：
　　　　　　　　
　　　　　　　　

　　　
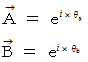
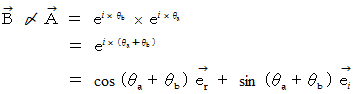
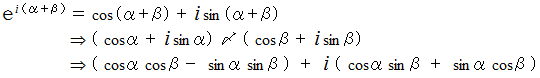
　　　したがって、
　　　　　　　　

（２） 点の回転写像を用いる証明法

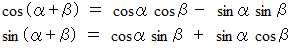
　 加法定理の最も簡単な証明法は、 点の回転写像を用いる方法だと思います。

　 原点からの距離が であるところの点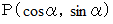 を原点を回転中心として反時計回りに 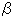ラジアン回転させる写像は、次のようなものです。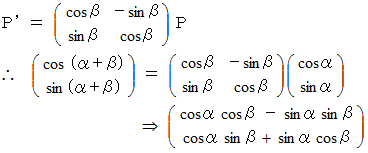

　　　　　

これは、 ズバリ加法定理の証明です。