(1) 母集団の平均の点推定
-
母集団の平均値は、 標本集団の平均値に近似します。
-
平均値
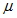 ( この値は公表されていない ) 、 標準偏差
( この値は公表されていない ) 、 標準偏差 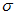 ( この値は公表されている ) の母集団から、 サンプル
( この値は公表されている ) の母集団から、 サンプル  個を無作為に抽出します。 そしてその標本の平均値を
個を無作為に抽出します。 そしてその標本の平均値を 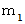 とします。 ここから先は実際にしなくていいのですが、そのサンプルを元に戻してから、また同じことをしてその平均値を
とします。 ここから先は実際にしなくていいのですが、そのサンプルを元に戻してから、また同じことをしてその平均値を 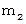 とします。 そのサンプルを元に戻してから、 また同じことをしてその平均値を
とします。 そのサンプルを元に戻してから、 また同じことをしてその平均値を 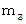 とします。 このようにしてたくさんたくさん非常にたくさん集めた標本平均の平均をとりますと、それは
とします。 このようにしてたくさんたくさん非常にたくさん集めた標本平均の平均をとりますと、それは 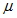 になります。横軸にそれぞれの標本平均値をとり、縦軸にその度数をとってグラフにします。 これを 「 標本平均についての確率分布 」 と言います。 するとそれは、 平均値
になります。横軸にそれぞれの標本平均値をとり、縦軸にその度数をとってグラフにします。 これを 「 標本平均についての確率分布 」 と言います。 するとそれは、 平均値 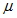 、 標準偏差
、 標準偏差  の正規分布になっています。
の正規分布になっています。したがって、 最初の調査の n 個の標本の平均(m1)を m として、
 と置くと、
と置くと、 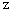 は「 標準正規分布 」に従います。
は「 標準正規分布 」に従います。標準正規分布表より、
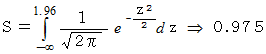
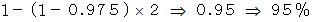
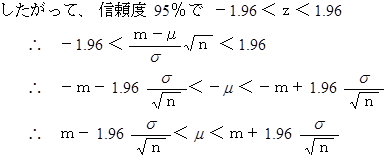
以上から、 母集団の平均値が明らかでなくて、 母集団の標準偏差が明らかになっているとき、 母集団の平均値 μ は95%の確率で
 に入ることがわかります。 m は標本平均です。 これを区間推定といいます。 区間推定は 「 標本の平均が m だから 母集団の平均値も m であろう。」 と推測する点推定のように単純なものではありません。
に入ることがわかります。 m は標本平均です。 これを区間推定といいます。 区間推定は 「 標本の平均が m だから 母集団の平均値も m であろう。」 と推測する点推定のように単純なものではありません。 以上の推定は、 母集団の平均値が不明ですが標準偏差が明らかになっている場合に用いられます。 しかし、 実際は母集団の平均値も標準偏差も明らかになっていないと思います。 そこで、 母集団の平均値を推定するために t 分布 が用いられます。
正規分布に従う母集団の平均値を μ とします。 そこから無作為に n 個の標本を採取します。 標本の平均が m で、 標準偏差が w であったとします。 この情報から μ を推定します。
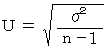
上記の t は 自由度 n−1 の t 分布 に従います。
例えば、 n = 101 のとき、 自由度100 の t 分布は 信頼度95%で、
− 1.9840 ≦ t ≦ 1.9840 なので、 次のようになります。
こうして、 母集団の平均は、 信頼度95%で、
にあることが推定できます。
-
母集団の分散は、 標本集団の不偏分散に近似します。
不偏分散とは、 標本の分散に
-
正規分布に従う母集団の、平均値を μ(未知でも既知でも可)とし、分散を σ2(未知)とします。 そこから無作為に n 個の標本を採取します。 標本の平均が m で、 不偏分散が U2 であったとします。 この情報から σ2 を推定します。
上記の T は 自由度 n−1 の カイ2乗 (x2) 分布 に従います。
例えば、 n = 10 のとき、 自由度 9 の カイ2乗分布 は 信頼度95%で、
2.70 ≦ x2 ≦ 19.0 なので、 次のようになります。
-
不良品含有率が
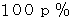 の製品を無作為に
の製品を無作為に  個抽出して不良品が何個(
個抽出して不良品が何個(  個 )入っているのかを調査しました。 同じことを何度も何度も繰り返して1000回に渡り調査をした後、 横軸に
個 )入っているのかを調査しました。 同じことを何度も何度も繰り返して1000回に渡り調査をした後、 横軸に  をとり 縦軸に 度数を1000で割った値 をとってグラフを作りました。 するとこのグラフは、 次の確率分布を持つ二項分布に近いものになります。
をとり 縦軸に 度数を1000で割った値 をとってグラフを作りました。 するとこのグラフは、 次の確率分布を持つ二項分布に近いものになります。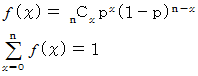
また、 このグラフは次の平均と標準偏差を持つ正規分布に近いものにもなっています。

そこで、
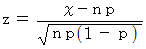 と置くと、
と置くと、 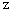 は 「 標準正規分布 」 に従います。
は 「 標準正規分布 」 に従います。標準正規分布表より、
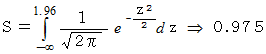
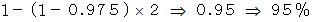
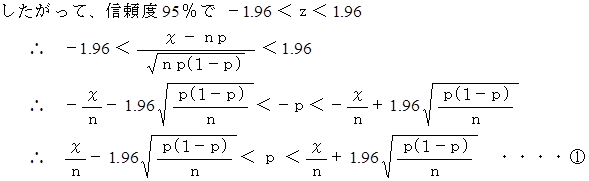
 について、
について、 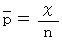 と置き、 ルート内の
と置き、 ルート内の 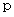 に関して
に関して 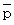 で近似すると、 次のようになります。
で近似すると、 次のようになります。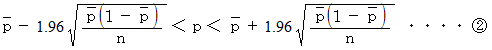
さて、 この調査では、 全体で、
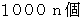 の標本を集めています。 このときに出てきた不良品の総計を
の標本を集めています。 このときに出てきた不良品の総計を 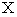 としますと、
としますと、 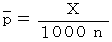 で具体的な
で具体的な 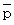 の値が決まりますので、 式
の値が決まりますので、 式 より
より 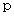 の範囲が求まります。
の範囲が求まります。 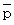 は「 標本比率 」、
は「 標本比率 」、 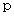 は「 母比率 」と言われますので、 今回は「 標本比率 」から「 母比率 」を推定したことになります。
は「 母比率 」と言われますので、 今回は「 標本比率 」から「 母比率 」を推定したことになります。では、 例題を解いてみましょう。
内閣支持率を1000人の成人を無作為に抽出して調査したところ、 ちょうど50%の人が支持していました。 この結果から、 内閣支持率を信頼度95%で推定してみましょう。 同じことを100回繰り返して、 横軸に支持者数として0人から1000人の自然数をとり、 縦軸に度数を100で割った数をとって、 グラフを作ったとしましょう。 するとこのグラフは、 次の平均と標準偏差を持つ正規分布に近いものになります。
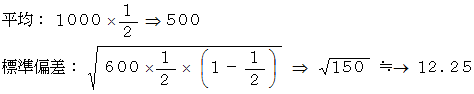
式
 より、
より、 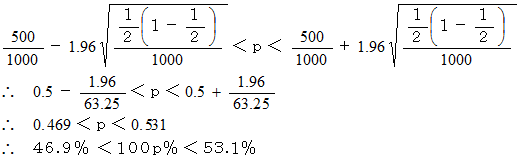
したがって、 内閣支持率は信頼度95%で
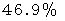 から
から 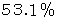 の間にあると推定できます。
の間にあると推定できます。では、 内閣支持率を信頼度95%で
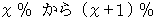 の狭い間にあると推定できるようにするためには、 さらに何人の調査を追加しなければならないでしょうか?
の狭い間にあると推定できるようにするためには、 さらに何人の調査を追加しなければならないでしょうか?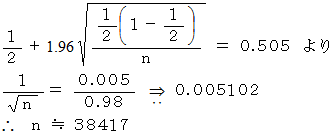
したがって、 さらに37417人の調査を行わなければなりません。
-
2つの母集団の平均値に有意差があるかどうかを検定するとき、 母集団の標準偏差が不明なときは、 t 分布を利用しますが、 母集団の標準偏差が明らかなときは正規分布を利用します。 ここでは、 正規分布を用いた母集団の平均差の推定の方法を紹介します。
母集団A : 平均値 μ1 分散 σ12
母集団B : 平均値 μ2 分散 σ22
母集団A の標本 : 標本数 n1 平均値 m1
母集団B の標本 : 標本数 n2 平均値 m2
確率変数 m1 − m2 は、 平均 μ1 − μ2 標準偏差
したがって、 信頼度 95% で、 次の式が成り立ちます。
|
母集団Aの標本 |
母集団Bの標本 |
|
128 |
113 |
| 136 | 126 |
| 138 | 132 |
| 140 | 135 |
| 147 | 139 |
| 154 | 156 |
|
平均値 140.5 |
平均値 133.5 |
母集団A の分散 : 64.0
母集団B の分散 : 144.0
式
以上より、 信頼度 95% で、 平均値の差は 1.11 〜 12.89 の範囲にあることが推定されました。 この範囲の中に0は入っていません。 したがって、 信頼度 95%で、 2つの母集団の平均値は異なると言えます。
 統計学 へ戻る
統計学 へ戻る