自由度３の適合検定
統計学 へ戻る
大学生のための数学 へ戻る
2013.11.14

　 同じ染色体にある２種類の形質遺伝子のことを、「 同染色体形質遺伝子ペア 」と言うことにしましょう。 そして、 ある植物の場合、 葉の色を決定する遺伝子と種の形を決定する遺伝子が「 同染色体形質遺伝子ペア 」であったとしましょう。 花の色については、 紫色が優性形質で赤色が劣性形質であり、 種の形については、 丸が優性形質であり、 長丸が劣性形質であるとします。 そこで、 花を紫色にする遺伝子を A 、 花を赤色にする遺伝子を a 、 種を丸くする遺伝子を B 、 種を長くする遺伝子を b とします。
　 ここに単種（非雑種）の２つがあり、 一方は優性種でもう一方は劣性種であるとします。 つまり、 優性種の持っている遺伝子は AABB であり、劣性種の持っている遺伝子は aabb です。 ここで、 この２つを交配させて雑種を作ります。 すると第１世代の雑種の持つ遺伝子は AaBb となり、 花は紫色で種は丸の表現形態になります。 では、 この第１世代を自家受精させると第２世代の表現形態の比率はどのようになるでしょうか？　
したがって、
　　　　紫花 かつ 丸種　：　紫花 かつ 長種　：　赤花 かつ 丸種　：　赤花 かつ 長種　は、
　　　９ ： ３ ： ３ ： １　になります。

第２世代の花480個について調査した結果は、 次のようなものでした。 　 理論値は、 270個 ： 90個 ： 90個 ： 30個 です。 しかし、 実際には遺伝子組み換えが起こるため理論どおりにはいきません。 この調査の結果から、 この花のこれらの形質についての優性遺伝は遺伝子組み換えを無視できる範囲にあるといえるでしょうか？

それを判断するためには、 自由度３のカイ２乗検定をすればいいのです。
　　　帰無仮説 ： 「 この標本は、 理論どおりになっている。」
　　　　　　
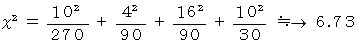
　 カイ２乗分布表を見ると、 自由度３で有意水準 の場合は、 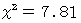になっています。 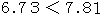ですから、 帰無仮説を棄却できません。 ということは、 遺伝子組み換えは無視できる範囲にあるといえます。

ちなみに、 自由度 のカイ２乗分布は、 次の式で与えられます。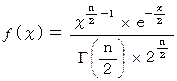
　　　　　
なお、 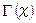はガンマ関数です。