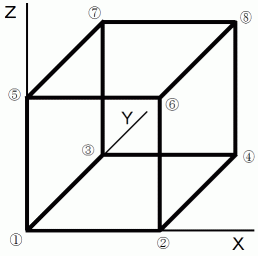
上図は
 ですが、 この立方体を8個くっつけ、 辺の長さが2倍で、 重心が
ですが、 この立方体を8個くっつけ、 辺の長さが2倍で、 重心が  の交点に存在する立方体を考えます。 そしてそれを
の交点に存在する立方体を考えます。 そしてそれを  と言うことにします。
と言うことにします。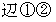 、
、 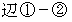 、
、  、
、 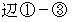 、
、  、
、 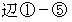 の長さを
の長さを 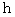 とし、
とし、  をそれぞれ起点とするベクトルを次のように表します。 そして、 これらのベクトルたちは力を表すものだと考えてください。
をそれぞれ起点とするベクトルを次のように表します。 そして、 これらのベクトルたちは力を表すものだと考えてください。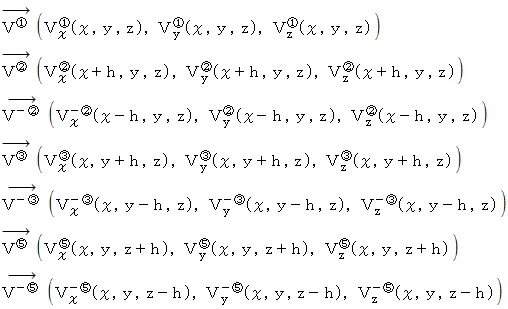
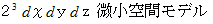 をZ軸のプラス方向から観察すると、 XY平面が見えます。 X軸に力を加えてXY十字を回転させようとするとき、 その力の
をZ軸のプラス方向から観察すると、 XY平面が見えます。 X軸に力を加えてXY十字を回転させようとするとき、 その力の 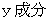 のみが回転に関与します。 そして、 力点が
のみが回転に関与します。 そして、 力点が  の領域では、 その力の
の領域では、 その力の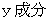 が正の数であれば、 反時計回りに回転し、 その力の
が正の数であれば、 反時計回りに回転し、 その力の 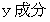 が負の数であれば、 時計回りに回転し、 力点が
が負の数であれば、 時計回りに回転し、 力点が  の領域では、 その力の
の領域では、 その力の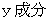 が正の数であれば、 時計回りに回転し、 その力の
が正の数であれば、 時計回りに回転し、 その力の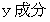 が負の数であれば、 反時計回りに回転します。 Y軸に力を加えてXY十字を回転させようとするとき、 その力の
が負の数であれば、 反時計回りに回転します。 Y軸に力を加えてXY十字を回転させようとするとき、 その力の 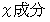 のみが回転に関与します。 そして、 力点が
のみが回転に関与します。 そして、 力点が  の領域では、 その力の
の領域では、 その力の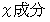 が正の数であれば、 時計回りに回転し、 その力の
が正の数であれば、 時計回りに回転し、 その力の 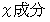 が負の数であれば、 反時計回りに回転し、 力点が
が負の数であれば、 反時計回りに回転し、 力点が  の領域では、 その力の
の領域では、 その力の 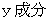 が正の数であれば、 反時計回りに回転し、 その力の
が正の数であれば、 反時計回りに回転し、 その力の 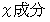 が負の数であれば、 時計回りに回転します。
が負の数であれば、 時計回りに回転します。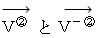 によるXY十字の回転の力のモーメントを考えると、 次のようになります。
によるXY十字の回転の力のモーメントを考えると、 次のようになります。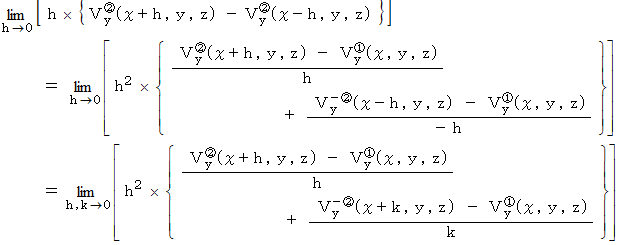
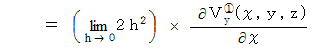
 によるXY十字の回転の力のモーメントを考えると、 次のようになります。
によるXY十字の回転の力のモーメントを考えると、 次のようになります。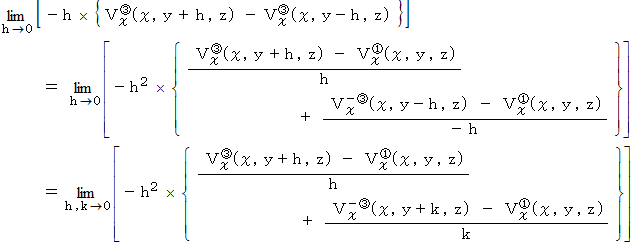
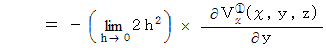
この2つの合計をとると、 次のようになります。
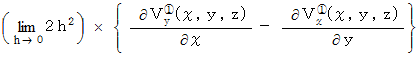
これはZ軸を右ネジの方向に回転させようとする力のモーメントの大きさです。 力のモーメントの向きはZ軸方向です。 したがって、 次のベクトルをもって、 YZ十字の回転を表すものと定義することにし、 これを「 Z軸の回転 」と言うことにします。
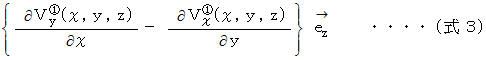
 をX軸のプラス方向から観察すると、 YZ平面が見えます。 Y軸に力を加えてYZ十字を回転させようとするとき、 その力の
をX軸のプラス方向から観察すると、 YZ平面が見えます。 Y軸に力を加えてYZ十字を回転させようとするとき、 その力の  のみが回転に関与します。 そして、 力点が
のみが回転に関与します。 そして、 力点が  の領域では、 その力の
の領域では、 その力の  が正の数であれば、 反時計回りに回転し、 その力の
が正の数であれば、 反時計回りに回転し、 その力の  が負の数であれば、 時計回りに回転し、 力点が
が負の数であれば、 時計回りに回転し、 力点が  の領域ではその力の
の領域ではその力の  が正の数であれば、 時計回りに回転し、 その力の
が正の数であれば、 時計回りに回転し、 その力の 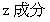 が負の数であれば、 反時計回りに回転します。 Z軸に力を加えてXY十字を回転させようとするとき、 その力の
が負の数であれば、 反時計回りに回転します。 Z軸に力を加えてXY十字を回転させようとするとき、 その力の 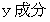 のみが回転に関与します。 そして、 力点が
のみが回転に関与します。 そして、 力点が  の領域では、 その力の
の領域では、 その力の 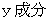 が正の数であれば、 時計回りに回転し、 その力の
が正の数であれば、 時計回りに回転し、 その力の 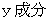 が負の数であれば、 反時計回りに回転し、 力点が
が負の数であれば、 反時計回りに回転し、 力点が  の領域では、 その力の
の領域では、 その力の 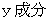 が正の数であれば、 反時計回りに回転し、 その力の
が正の数であれば、 反時計回りに回転し、 その力の 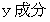 が負の数であれば、 時計回りに回転します。
が負の数であれば、 時計回りに回転します。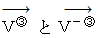 によるYZ十字の回転の力のモーメントを考えると、 次のようになります。
によるYZ十字の回転の力のモーメントを考えると、 次のようになります。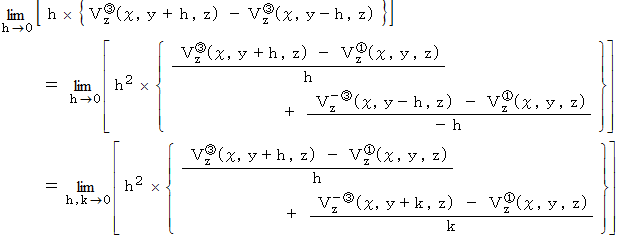
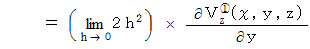
 によるYZ十字の回転の力のモーメントを考えると、 次のようになります。
によるYZ十字の回転の力のモーメントを考えると、 次のようになります。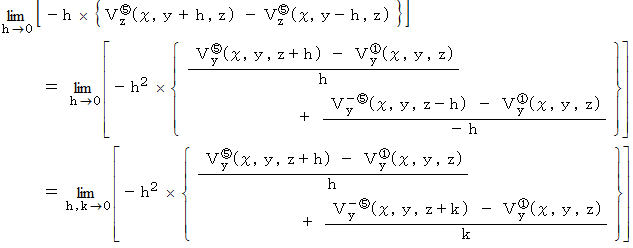
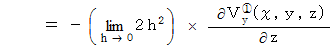
この2つの合計をとると、次のようになります。
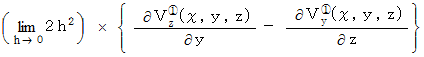
これはX軸を右ネジの方向に回転させようとする力のモーメントの大きさです。 力のモーメントの向きはX軸方向です。 したがって、 次のベクトルをもって、 YZ十字の回転を表すものと定義することにし、 これを「 X軸の回転 」と言うことにします。
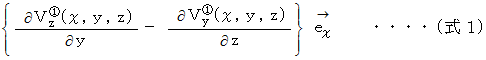
同様にして、「 Y軸の回転 」は次のようになります。
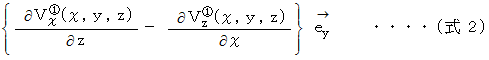
最終的に、
 を加えたものを、「 回転 」と言うことにします。
を加えたものを、「 回転 」と言うことにします。蛇足ですが、 以上のように3つの力のモーメントを加えると、 新しいベクトルが合成され、 新しい向きと大きさを持つ力のモーメントが出来上がります。 これは力の合成と同様です。 合成された力が幻ではなく実在するのものであるように、 合成された力のモーメントも、 実在するものです。 剛体の回転の角速度についても、 力のモーメントの合成と同様のことを言うことができますので、 ジャイロ効果( 科学博物館の体験コーナーによくある、 回転椅子に座って回転する車輪を両手で持って自転車に乗っているような状況を作り、 そこから車輪を左右の方向に傾けると、 傾けた方向に椅子が回り始める現象 )を説明するための原理となっています。
 ベクトル解析 へ戻る
ベクトル解析 へ戻る