ボウリングのレーンの上を移動するボールは、 真剣に転がっていない。 滑り半分の移動である。 真剣に転がるとは、 １回転したらに直径に をかけた距離だけ移動することである。 真剣に転がるには、 しっかりとした摩擦と垂直抗力が必要だ。

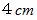　 底面の直径 、 長さ 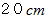の鉄の円柱がある。 中心をくり抜いて、 底面の直径 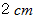、 長さ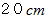 の円柱と、 それ以外の部分に２分する。 この２つを、 傾斜が10度の真剣に転がる傾斜を転がしてスピード（ ）を比べてみよう。

　 内部がくり抜かれた方は、 転がりの半径（ ）が２倍で、 質量（ ）が４倍で、 転がりの慣性モーメント（ ）が７倍である。

　　　　　　　　　　慣性モーメントは、 それぞれ次のようになる。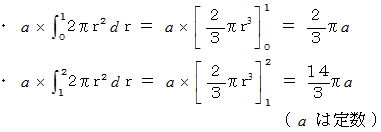
　　　　　　　　　　　　　　　　　

エネルギー保存の法則を表す式は次のようになる。
　　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　

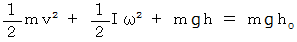
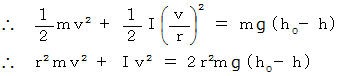
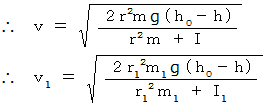
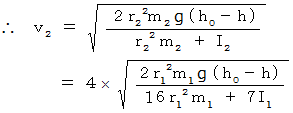
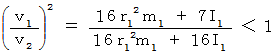
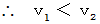
したがって、 内部がくり抜かれた方が速く転がることが解った。


　 底面の直径 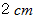、 長さ 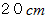の円柱と形や質量が同じで、 転がりの慣性モーメントが２倍の円柱の転がる速さ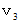（ ）は次のようになる。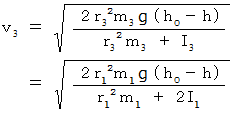
　　　　
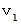　 と 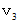とを比べると、 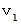の方が大きいことがわかる。 したがって、 形や質量が同じであれば、 円柱は転がりの慣性モーメントが小さいほど、 速く転がることがわかる。