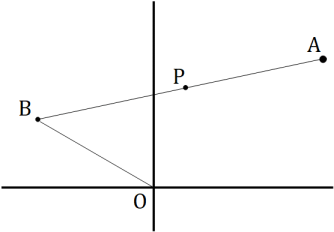
点 \( P\left(\ p_x,\ p_y\ \right) \) に対して点 \( A \) は 点 \( B\left(\ b_x,\ b_y\ \right) \) と対称な位置にあります。
点 \( A \) の座標は次のベクトル式で求めることができます。
　　　\( \scriptsize\overrightarrow{OA}\)　＝　\( \scriptsize\overrightarrow{OB}\ \) ＋ 2 × \( \scriptsize\overrightarrow{BP} \)
　　　　　＝　\( \left(\ b_x,\ b_y\ \right) \)　＋　2 × \( \left(\ p_x-b_x,\ p_y-b_y\ \right) \)
　　　　　＝　\( \left(\ 2p_x-b_x,\ 2p_y-b_y\ \right) \)

別解として次のような方法もあります。
　　　点 \( A\left(\ a_x,\ a_y\ \right) \) と置く。
　　　点 \( P \) は線分 \( AB \) の中点だから次の式たちが成り立つ。
　　　　　　\( p_x\ = \frac{a_x\ +\ b_x}{2} \) ，　　\( p_y\ = \frac{a_y\ +\ b_y}{2} \)
　　　　　　よって、　\( a_x\ =\ 2p_x-b_x \) ，　　\( a_y\ =\ 2p_y-b_y \)