(1) 外回りのギャップ
-
私たちは、 しばしば、 半径の比較的短い 内円と外円の円周の長さの比 のイメージでもって、 半径の比較的長い 内円と外円の円周の長さの差 をイメージしてしまいますが、 高度 1000 m の上空 と 高度 2000 m の上空 を、 2台のジェット機が 時速 800 km で飛んで地球を一周するとき、 飛行時間の差は、 たったの 28秒 であることを証明してみましょう。
地球の半径に 1000 m を加えたものを
 とすると、 2つの円周の差は次のようになって、 これから飛行時間差が求まります。
とすると、 2つの円周の差は次のようになって、 これから飛行時間差が求まります。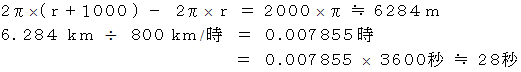
-
私たちは、 しばしば、 円形の物は膨張すると横幅だけが広がると勘違いしてしまいますが、 50円玉が熱膨張すると、 内側の穴が大きくなることを証明してみましょう。
50cm の針金を1本用意してください。 その両端をくっつけて輪を作ってください。 その輪を暖めてみましょう。 針金は膨張して長くなり、 輪が 102% に拡大します。 輪の内円の直径も、 輪の外円の直径も、 針金の太さも、 すべて 102% に拡長しています。
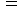 「 重力場 」
「 重力場 」-
私たちは、 しばしば、 空気抵抗の大きさや浮力を質量の小ささであると勘違いしてしまいますが、 重い物 も 軽い物 も 同じ速さで落ちることを証明してみましょう。
この問題は、 空気の抵抗がないことを前提にしています。 また、 初速が等しいことを前提にしています。 また、 地球の表面付近での2つの物質の落下であることを前提にしています。「 重い物 も 軽い物 も 同じ速さで落ちる 」を 正確に書くと、「 真空中の均一な重力場の中では、 質量が異なる2つの物質は、 落下するとき、 同等な加速度運動を行う。」となります。
証明には、「 ニュートンの運動方程式 」と「 ニュートンの万有引力の法則 」を使います。
ニュートンの運動方程式 :
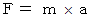
ニュートンの万有引力の法則 :
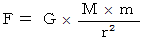

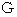 は万有引力定数です。
は万有引力定数です。万有引力の法則より、 地球の表面付近での重力は次のように表されます。
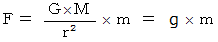



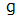 は地球の表面付近の一様な重力場を表します。
は地球の表面付近の一様な重力場を表します。この場合、
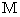 は 地球の質量、
は 地球の質量、  は 地球の半径です。
は 地球の半径です。 の式の意味は、 次のようなものです。
の式の意味は、 次のようなものです。地球の表面付近での重力
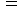 地球の表面付近の一様な重力場
地球の表面付近の一様な重力場 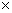 質量
質量運動方程式より、






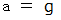
以上より、 質量に関係なく、 すべての物質の地球の表面付近での落下時の加速度は一定で、 地球の表面付近の一様な重力場と等しくなっている、 と言うことができます。
「 地球の表面付近の一様な重力場 」は、「 重力加速度 」と言われています。 しかし、 これでは、 ペンネームだけが先行して、 本人の本当の姿が見えなくなっているように思います。
「 一様な重力場 」と「 加速度 」とは区別のつかないものであるという主張がアインシュタインによってなされ、 これは今日「 等価原理 」と言われています。
-
運動摩擦力の大きさは、 物質の速さには関係なく、 質量に比例します。 したがって、 氷の上を滑るカーリングのストーンの質量が20kgから40kgに増えると、 初速が同じでもブレーキがよくかかるので短い距離しか滑らない、 と私たちは考えてしまいがちですが、 初速が同じならば質量に関係なく同じ距離と時間滑ることを証明してみましょう。
力学の基本は「 運動方程式を立てろ! 」です。
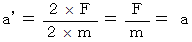
-
120km 離れた折り返し点まで、 行きは 時速 40km、 帰りは 時速 60km の速さで、 往復しました。 このとき、 平均速度は 時速 50km ではないことを示します。
距離
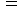 速さ
速さ 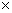 時間 の公式より、 次の式たちが成り立ちます。
時間 の公式より、 次の式たちが成り立ちます。
したがって、 平均時速は次のようになります。

別の解法として、 次のような式もあります。
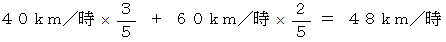
-
次の説明は間違っています :
質量
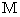
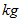 の地球の中心から
の地球の中心から 
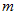 離れた所を速さ
離れた所を速さ 
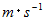 で等速円運動している質量
で等速円運動している質量 
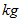 の人工衛星がある。 このとき、 人工衛星の慣性モーメント
の人工衛星がある。 このとき、 人工衛星の慣性モーメント 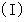 は
は 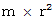 で、 角速度
で、 角速度 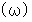 は
は 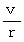 である。 人工衛星の速さと軌道半径とには、 角運動量保存の法則より導かれる、 次のような関係がある。
である。 人工衛星の速さと軌道半径とには、 角運動量保存の法則より導かれる、 次のような関係がある。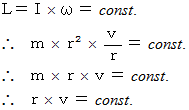
したがって、 人工衛星の速さは、 軌道半径の
 に比例している、 つまり、 軌道半径に反比例している。 この条件を保ちながら、 人工衛星は、 軌道半径や速さを変更しながら地球の周りを回っている。
に比例している、 つまり、 軌道半径に反比例している。 この条件を保ちながら、 人工衛星は、 軌道半径や速さを変更しながら地球の周りを回っている。間違いを訂正します :
人工衛星は、 一度安定軌道に乗ってしまったら、 いつまでもその軌道を等速で飛び続けます。 また、 人工衛星の速さは、 軌道半径の
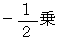 に比例します。
に比例します。人工衛星の公転は剛体の回転ではなく、 質点の回転移動とみなされますので、 慣性モーメントはありません。 人工衛星の移動の様式は、 次の2つの式に従います。
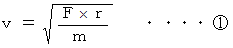
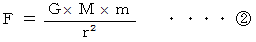
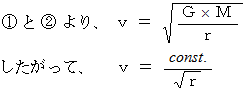
-
立体角の定義を次のように勘違いしている人があります。 間違いを指摘してください。
- 「 底面積
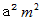 、 母線の長さ
、 母線の長さ  の円錐の側面の内面が頂点の周辺に形成するコーン状の立体角の大きさは
の円錐の側面の内面が頂点の周辺に形成するコーン状の立体角の大きさは  である。 母線とは円錐の頂点と底面の円の縁上の1点を結ぶ直線のことである。 」
である。 母線とは円錐の頂点と底面の円の縁上の1点を結ぶ直線のことである。 」間違いを指摘します :
半径
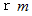 の球を中心からある角度で切り出したときの円錐様立体の底面 ( 曲面 ) の面積が
の球を中心からある角度で切り出したときの円錐様立体の底面 ( 曲面 ) の面積が  になるときの角度を「 立体角 」といい、 その大きさを
になるときの角度を「 立体角 」といい、 その大きさを  で表します。 あなたの定義では、
で表します。 あなたの定義では、  は、 本当の
は、 本当の  よりも大きくなってしまいます。
よりも大きくなってしまいます。 哲学と物理学 へ戻る
哲学と物理学 へ戻る