角速度は、 回転の方向と速さから成るものです。 ちなみに、 速度は、 移動の方向と速さから成ります。 円盤が正面から見て反時計方向に １ 秒間あたりθラジアン回転している場合、 角速度の向きは、 円盤に対して直角で観察者に対して真っ直ぐに向かってくる方向になり、 角速度の大きさは、 θ （ 秒^−１ ） になります。


　　　　　　　　　　　

　 地球のイメージは、 左側です。 なぜなら、 地球の自転軸は１つだからです。 右側は自転軸が２つあるイメージです。 下図は、 ２つの自転軸のイメージです。

　　　　

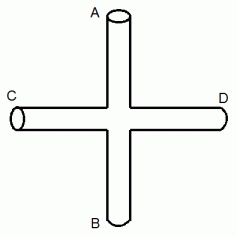
　 ＡＢ軸は、 角速度の向きが Ｂ → Ａ の方向に回転しているとします。 すると、 Ｃは次第に手前に移動しながら右側に回転していきます。
　 ＣＤ軸は、 角速度の向きが Ｄ → Ｃ の方向に回転しているとします。 すると、 Ｂは次第に手前に移動しながら上側に回転していきます。

　 ではここで問題です。 ２つの自転の角速度の大きさが等しいときはどんなイメージになるのでしょうか？

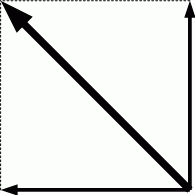
割りばしで上図のようなものを作ってやってみてもいいと思います。 結局、 下図のイメージになります。

　　　　

　 なぜなら、 ２つの軸の角速度ベクトルを合成したものが、 総合的な回転運動を表す角速度ベクトルになるからです。

　　　　　　

　 回転の合成のしくみについては、 大学生のための物理学 ＞ 剛体力学 ＞ 回転の合成と分解　 をご覧ください。