2つの平均値の間に有意な差があるかどうかを調べるのが、 t 検定 です。
・ 単純 t 検定
理想的な母集団の平均値 と 標本から推測する母集団の平均値 とを比べる。
・ 関連2群標本 t 検定
母集団の平均値 と 母集団に属する子集団の平均値 とを比べる。
・ 独立2標本 t 検定 ( 分散が等しいことが条件 )
標本Aから推測する母集団の平均値 と 標本Bから推測する母集団の平均値 とを比べる
・ 単純 t 検定
理想的な母集団の平均値 と 標本から推測する母集団の平均値 とを比べる。
・ 関連2群標本 t 検定
母集団の平均値 と 母集団に属する子集団の平均値 とを比べる。
・ 独立2標本 t 検定 ( 分散が等しいことが条件 )
標本Aから推測する母集団の平均値 と 標本Bから推測する母集団の平均値 とを比べる
-
350cc 入りとラベルに書かれてありますので、 量が間違っていたら困ります。 生産されたジュース9本をサンプルとして抽出し調査したところ、 1 本中の量の平均値は 346cc、 不偏分散は 36cc でした。 危険率 5%の条件下で、 量が間違っていると断言できなければ、 生産を続行してもよいというルールになっているのですが、 生産を続行してもよいでしょうか?
-
仮説 : 生産されるジュースの量は 1 本あたり 350cc である。
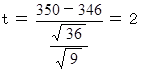
t 分布表より、 自由度8のとき、 危険率5% で 2.306 。
2 < 2.306 ですので、 仮説は否定できません。
したがって、 危険率 5%の条件下で、 生産されるジュースの量は 1 本あたり 350cc ではないと断言できません。 よって、 このまま生産を続行してよろしいということになります。
 統計学 へ戻る
統計学 へ戻る