【 問 題 1 】
-
女性が5人、 男性が3人いる。 無作為に一列に並ぶとき、
男性が隣りどうしにならない確率を求めよ。
-
男1 男2 男3 男4 男5 女1 女2 女3 の8人とします。
まず、 全員が一列に並ぶ場合の数を求めます。
それは 8! です。
次に、 問題の場合の数を求めます。
まず、 女性5人が一列に並ぶ場合の数を求めます。
それは 5! です。
次に、 女性5人の列の間に前後を含めて計6個の椅子を配置します。
その6個の椅子に、 男性3人が着く場合の数を求めます。
それは 6C3 × 3! です。
したがって答えは、
( 5! × 6C3 × 3! ) ÷ 8! =→ 5 / 14
-
男性が5人、 女性が3人いる。 8人掛けの丸テーブルの席に全員が着くとき、
女性が隣りどうしにならない確率を求めよ。
-
男1 男2 男3 男4 男5 女1 女2 女3 の8人とします。
まず、 テーブルの席の着き方のすべての場合の数を求めます。
それは 7! です。
 円順列の公式 : (n−1)!
円順列の公式 : (n−1)!次に、 問題の場合の数を求めます。
まず、 男性5人が10人掛けのテーブルに 1 席ずつ空けて着く場合の数を求めます。
それは 4! です。
次に、 空いた席に3人の女性を配置する場合の数を求めます。
それは
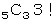 です。
です。したがって答えは、
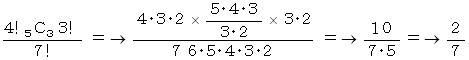
 確率 へ戻る
確率 へ戻る