（１）　ベクトルの写像の例

　 ２次元直交座標系において、 原点を起点とするベクトルを時計回りに θ ラジアン 回転させる 演算テンソルの表現行列 （ 私によるネーミング ） は次のように表されます。
　　　　
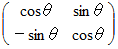
　 たとえば、 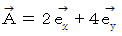というベクトルを時計回りに90度回転させて 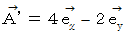を得る演算を、 次のように表わすことにします。。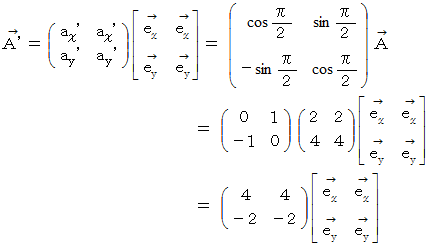
　　　　


（２）　座標変換について

　 座標変換とは基底変換が起因する座標値の変換です。 原点が原点に変換される場合の座標変換は、 原点を起点とし座標点を終点とするベクトルの表示方法の変換であるとも言えます。

　 座標変換では、 基底変換テンソル （ 私によるネーミング ） の表現行列 と 座標変換テンソル （ 私によるネーミング ） の表現行列 とは逆行列の関係になっています。


（３）　本文

簡明化のため、 ２次元空間で考えることにします。
静止座標系において、 質点が曲線軌道を描いて速さを変化させながら移動しています。

　 等速自転座標系 とは、 一般には 等速回転座標系 と言われているもので、 静止座標系に対して一定の角速度 で反時計回りに自転している座標系のことです。 等速自転座標系の基底の要素の大きさは、 静止座標系の基底の要素の大きさと同じです。 静止座標系と等速自転座標系の原点が同じ位置にある場合、 静止座標系から等速自転座標系への基底変換と座標変換は、 それぞれ次のような式になります。

　　基底変換テンソルを用いた基底変換式 ：
　　　　

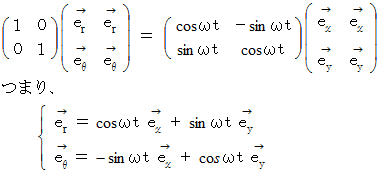
　　座標変換テンソルを用いた座標変換式 ：
　　　　

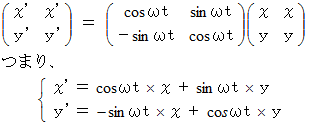
　 観察している物質が等速円運動をしている場合、等速自転座標系 は 随伴自転座標系 と同じになります。