(1) 偏差 と 偏差値 と 標準偏差
-
標準偏差は平均値と共に母集団の形を見るもので、 偏差や偏差値は、 個が母集団のどのあたりに属しているのかを見るものです。
標準偏差とは、 偏差の2乗の平均の平方根の正の値である。
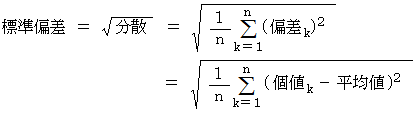

偏差値よりも次の偏差比のほうが解りやすくねえ?
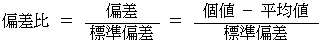
-
正規分布をしている母集団の確率密度
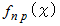 は、偏差比を確率変数として次のように表されます。
は、偏差比を確率変数として次のように表されます。
このとき、 偏差比の絶対値が
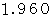 以上 の場合は、「 母集団の5%以内の特殊な存在 」になります。 いわゆる「 2SD( Standard
deviation )を超えている。」というやつです。
以上 の場合は、「 母集団の5%以内の特殊な存在 」になります。 いわゆる「 2SD( Standard
deviation )を超えている。」というやつです。標準偏差が小さければ小さいほど
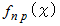 のグラフは背が高くなります。( このグラフは確率変数が個値である正規分布のグラフとは少し異なりますので、 標準偏差によって横幅が変化することはありませんし、 必ず偏差比が
のグラフは背が高くなります。( このグラフは確率変数が個値である正規分布のグラフとは少し異なりますので、 標準偏差によって横幅が変化することはありませんし、 必ず偏差比が  のところを軸として対称になっています。)
のところを軸として対称になっています。) 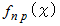 を偏差比のマイナス無限大からプラス無限大の範囲で積分すると
を偏差比のマイナス無限大からプラス無限大の範囲で積分すると  になります。
になります。-
統計学には、 母集団 や 抽出標本 や 事象 という概念がありますが、 それは集合論から発生しています。 集合論とは、 属するかどうか、 属するものがあるかないか を問う論理学です。
統計学では、 個は全体のどのあたりに属しているのかを解析します。 個は全体の標準的な位置にあるとの仮説を立てて、個は全体の特別な位置にあると言い切れるのかどうかを問う方法を検定といいます。
また、 統計学では、 標本を集めて集計分析し、 母集団の性質を推測します。 これを推定といいます。
統計学では、 確率という手法が用いられます。 確率とは事象が起こりうる頻度のことです。
確率分布は、 パターン化されており何十種類とあります。 その中で、 自然界で最も多いのが正規分布です。 個値そのものが正規分布に従っているものもあれば、 個値の対数が正規分布に従う場合もあります。 また、 母集団が正規分布のとき、 そこから抽出した標本の値にも確率分布があります。 たとえば、 カイ2乗分布がその例です。 統計学は、 パターン化された確率分布をしている集合を対象にして発展してきましたが、 確率分布の状態が不明な集合に対する統計学は、 ノンパラメトリックと言われます。
確率論には、 期待値 という概念があります。 それは、 ある試行によって得られる数値に確率をかけたもので、 試行によって得られる数値の予想値になります。 母集団から無作為にデーターを抽出したとき、 その平均値の期待値は、 母集団の平均値になります。
 統計学 へ戻る
統計学 へ戻る