２次元座標系にスカラー場：f ( x, y ) が存在します。
　もし、z ＝ f ( x, y ) として３次元座標系で考えると曲面が形成されます（ これを曲面Ｆとします ）が、今回はあくまでも　z ＝ 0　の x y 平面で考えてください。

　f ( x, y ) ＝ Ｃ（ 定数 ）で表される曲線 f をグラフで表し、点Ｐにおいてそれと直角に交わる直線 L を引きます。

　　　

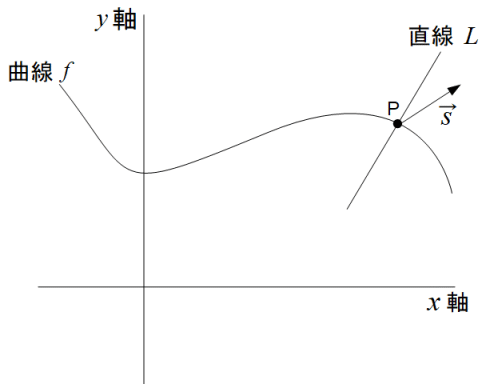
　曲線 f よりも上側に行くにつれ次第に f ( x, y ) の値は大きくなり、曲線 f よりも下側に行くにつれ次第に f ( x, y ) の値は小さくなるとします。曲線 f は曲面Ｆの等高線（ 等位線 ）になります。

　さて、勾配とは、曲面上のある点において、曲面の傾きが最大になる方向を向き、その点における曲面の最大の傾きの大きさと等しい大きさを持つベクトルのことです。２次元スカラー場の勾配は x y 平面上の２次元ベクトルです。勾配を二次元平面で表現するには、曲面の勾配の射影をとって、方向は射影の方向どおり、大きさは勾配の大きさに変更します。

　二次元平面で表現する f ( x, y ) の勾配： ∇f ( x, y )　の向きは直線 L に平行です。

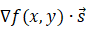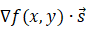　ここで、点Ｐを起点とする大きさが１のベクトル を考え、二次元平面で表現する f ( x, y ) の勾配 との内積 をとります。これは の方向への局面Ｆの傾きを表します。 は方向微分と言われます。