衝突する2つの物質のうち、一方が塑性変形をし他方が弾性変形をする場合には、比較的簡単に衝突の力を求めることができます。
静止している壁に対して等速直線運動をしている質量
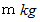 、 速さ
、 速さ 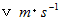 の弾丸が壁に衝突しました。 衝突してから
の弾丸が壁に衝突しました。 衝突してから 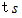 の時間後に、 弾丸は塑性変形せずに先端が壁の中に
の時間後に、 弾丸は塑性変形せずに先端が壁の中に 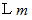 埋まった所で静止しました。 弾丸が等加速度運動をして静止したものと仮定して、 弾丸に
埋まった所で静止しました。 弾丸が等加速度運動をして静止したものと仮定して、 弾丸に 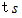 の時間どれだけの力が作用したのかを考えてみましょう。
の時間どれだけの力が作用したのかを考えてみましょう。弾丸が壁に衝突してから静止するまでの加速度
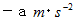 は、 次のようになります。
は、 次のようになります。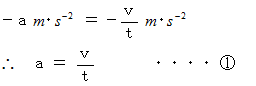
弾丸が壁に衝突してから静止するまでの距離に関して、 次の式が成り立ちます。
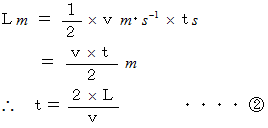
※ 詳細に記述すると
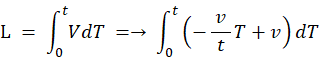
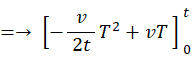
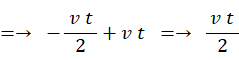
 を
を  に代入すると、
に代入すると、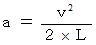
これをニュートンの運動方程式に代入すると、
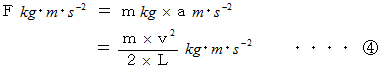
 は、弾丸が壁に衝突してから静止するまでの間、壁が弾丸に作用した一定の力です。衝撃力と言えます。
は、弾丸が壁に衝突してから静止するまでの間、壁が弾丸に作用した一定の力です。衝撃力と言えます。ここで、 弾丸の運動エネルギーを
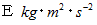 とすると、 次の式が成り立ちます。
とすると、 次の式が成り立ちます。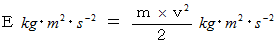
これを
 に代入すると、
に代入すると、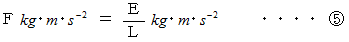
 が壁が弾丸に作用した力ですが、 作用反作用の関係から
が壁が弾丸に作用した力ですが、 作用反作用の関係から  は弾丸が壁に作用した力であるとも言うことができます。 これから、 衝撃力の大きさは、 静止している衝突される物質に対する衝突してくる物質の運動エネルギーに比例していることがわかります。
は弾丸が壁に作用した力であるとも言うことができます。 これから、 衝撃力の大きさは、 静止している衝突される物質に対する衝突してくる物質の運動エネルギーに比例していることがわかります。また、 この間の力積は次のようになります。
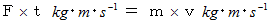
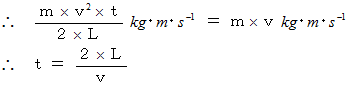
したがって、 弾丸が壁に当たってから静止する時間は
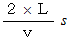 で、
で、  と合います。
と合います。コメント : 力積は運動量の差です。 なぜなら、 次の式が成り立つからです。
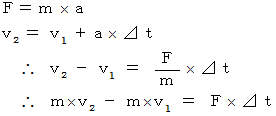
 力学 へ戻る
力学 へ戻る