弦を振動させたときに生じる定常波の中では、 その振動数の整数倍のたくさんの張線横波が弦の一端から他端までの間を同じ速さで行ったり来たりしています。 弦を振動させたときに生じる音の高さは、 弦の定常波の振動数によって決まり、 定常波の振動数は、次の式によって決まります。

今回は、 次の式が成り立っているしくみを学んでみましょう。

次の図を見てください。 張線横波が右に向かって速さ
 で移動しているとします。
で移動しているとします。  後 に波は
後 に波は  だけ右側に変位していますが、 その時、 4か所の媒質の位置は線で表したように移動します。一番右の媒質だけは上方に移動します。
だけ右側に変位していますが、 その時、 4か所の媒質の位置は線で表したように移動します。一番右の媒質だけは上方に移動します。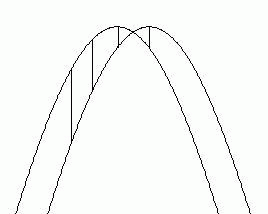
これを波と同じ速度で移動している観察者が見ると、 媒質たちが波線上を左に向かって移動しているように見えます。
ここで、 波の腹(頂点)付近の微小部分が微小時間に移動するのを、 波と同じ速度で移動している観察者の立場で見てみます。
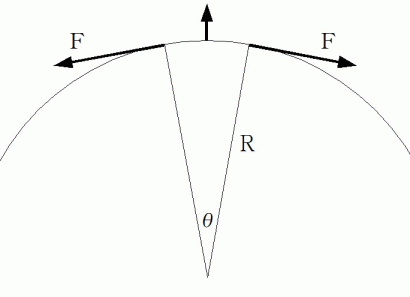
波の媒質の微小部分の曲率半径を
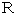 とし、 媒質の微小部分の両端と曲率円の中心を結んでできる弧の中心角を
とし、 媒質の微小部分の両端と曲率円の中心を結んでできる弧の中心角を  とし、 媒質の綿密度を
とし、 媒質の綿密度を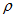 とすると、 媒質の微小部分の質量は
とすると、 媒質の微小部分の質量は 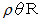 になります。 媒質の微小部分は速さ
になります。 媒質の微小部分は速さ  で曲率円周上を反時計方向に回転しています。 そして、 媒質の微小部分の両端には大きさ
で曲率円周上を反時計方向に回転しています。 そして、 媒質の微小部分の両端には大きさ  の張力が作用しています。
の張力が作用しています。ここで向心方向の運動方程式を立てます。 遠心力は公式
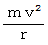 より、
より、 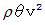 になります。 向心力は媒質の微小部分の両端に作用する張力の遠心力方向と反対の方向の成分の和であり、 次のようになります。
になります。 向心力は媒質の微小部分の両端に作用する張力の遠心力方向と反対の方向の成分の和であり、 次のようになります。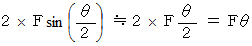
したがって、 向心方向の運動方程式は次のようになります。
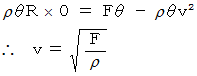
 基礎物理学 へ戻る
基礎物理学 へ戻る