日曜の朝はバロックです。 ビバルディの「 調和の幻想 」などはピッタリの気分です。

　 ドの音の振動数を 24 としたときの、 それぞれの音階の振動数の比

	ド	レ	ミ	ファ	ソ	ラ	シ
１オクターブ 低	12		15	16	18	20
	24	27	30	32	36	40	45
１オクターブ 高	48	54	60	64	72	80	90
２オクターブ 高	96	108	120	128	144	160	180

　 平板の少し上に弦を張り、 ギターのように指で弦を抑えることによって振動する弦の長さを自由に調節できるようにします。 開放弦で弾いた音を１オクターブ低いドの音とし、 弦の長さを とします。
　 弦の張り具合が一定のときは、 その弦が作る音の振動数は弦の長さに反比例します。 弦の長さに対応する弦の振動数および音階は次のようになります。

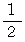
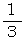
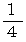
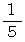
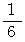
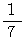
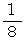
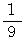
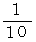
24	36	48	60	72	84	96	108	120
ド	ソ	ド	ミ	ソ	？	ド	レ	ミ

振動数の数列は公差12の等差数列になっています。
　 弦の長さを 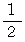、 、 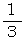、 　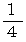と 短くしていきますと、 その弦が振動して奏でる音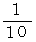は までは 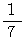以外すべて全音階の音になります。
　　　　　　
　 上記の数列は「 調和数列 」と言われます。 調和数列の各項は前後の項の 調和平均（ 逆数の平均の逆数 ）になっています。 たとえば、 第３項は次のようになっています。
　　　　　　
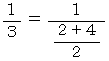
調和数列 とは各項の逆数が等比数列になっている数列のことです。
　　　　　　　※ 参考： 大学生のための数学 ＞ 数理論 ＞ 自然数の逆数の数列

　 弦の張り具合が一定のときは、 ド と １オクターブ高いド の弦の長さは ２：１ です。 ２ と １ の調和平均は ３分の４ です。 弦の長さの比が ２：4/3：１、 つまり、 ６：４：３ ならば、 その弦が作る音の振動数比は 1/6：1/4：1/3 つまり ２：３：４ になります。 ド と ソ と １オクターブ高いド の振動数比は ２：３：４ です。 ソ は ド と １オクターブ高いド のちょうど中間の高さの音です。

　　　　※　ド と ミ と ソ と １オクターブ高いド の振動数比は ４：５：６：８

　解放弦の長さを 1 として、その音をドとすると、音階を弾くために元端からどれくらい離れた所を指で順番に押さえていく必要があるかを示します。
　　　ド：　1 （24/24）
　　　レ：　8/9 （24/27）
　　　ミ：　4/5 （24/30）
　　　フ_ァ：3/4 （24/32）
　　　ソ：　2/3 （24/36）
　　　ラ：　3/5 （24/40）
　　　シ：　8/15 （24/45）
　　　ド：　1/2 （24/48）