「うなり」
音楽と物理学 へ戻る
ばいおりんの日常的物理学文集 へ戻る
2012.04.04

　 ギターを使って、 音の「 うなり 」を体験してみましょう。「 うなり 」とは、音高（ ピッチ ）がわずかに異なる２つの音が鳴っているとき、 周期的に表れる音の強弱のことです。

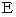
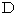
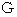
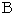
　 ギターは、 第６弦（ 最も太い弦 ）から順に、 解放弦が 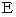の音名になっています。 第 弦 と 第 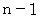弦 との振動数の比はおよそ 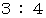の関係になっています。 ただし、 第３弦 と 第２弦 との振動数の比だけはおよそ 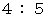です。

　 うなりを体験するには、 きちんと調弦されたギターの 第３弦 と 第２弦 以外 の隣り合う２つの弦を選びます。 そしてハーモニックという技法で音を鳴らします。 ハーモニックとは、 左手の指で弦に軽く触れてから右手で弦を弾(はじ)き、 その直後に左手の指を離すことによって鳴る、 高い神秘的な音のことです。 たとえば、 第６弦 と 第５弦 を選んだとしましょう。 まず、 第６弦のナットから全長の４分の１の所（ ５フレットの所 ）でハーモニー音を出します。 解放弦の音よりも２オクターブ高い Ｅ の音になります。 その直後に、 第５弦のナットから全長の３分の１の所（ ７フレットの所 ）でハーモニック音を出します。 同じピッチの音になります。 第５弦をわずかに緩めたり張ったりして「 うなり 」の程度を変化させてみてください。 最後は、 第５弦を「 うなり 」のない状態から、 若干張ってわずかに「 うなり 」があるとことろで終了してくだい。 きちんと調弦されたギターに戻してやるのです。

　　　　　　　　

　　　　　　　　

　　　　　　　　


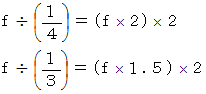
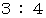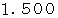　「 うなり 」が消えるところが、 ２つの音が全く同じ高さ（ ピッチ ）になったところです。 こうして、「 うなり 」がないようにギターを調弦していきますと、 きちんとした調弦にはなりません。 なぜなら、 ギターは純正調楽器ではなく、 平均律楽器だからです。 ギターの 第３弦 と 第２弦 以外の隣り合う２つの弦の振動数の比は、 よりも若干比率が大きくなっているのです。 それは、 ５度の和音において、 ド の音の振動数比を とすると、 ソ の音の振動数比は、 純正調は 、 平均律は 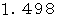になっているからです。（ ソ の音 と １オクターブ高いド の音の音程は ４度 です。）



十進BASIC のプログラムを使って、「 うなり 」を視覚化してみましょう。

＜ プログラム その１ ＞ 　 a = 1. 12　から初めて 0. 04 ずつ小さくしていき、 最後は、 1. 02　　1. 01　　1. 00　で、
「 うなり 」が消失します。


＜ プログラム その２　（ 振動数の差 ＝ １秒間あたりのうなりの回数 ） ＞ 　 a = ３　から初めて １ ずつ小さくしていき、 最後は０で「 うなり が消失します。



（ 付 録 ） うなりの正体

波動関数は次のように表されます。
　　　　

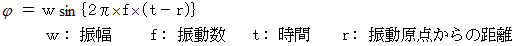
振幅が で振動数の差が 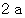の２つの波を合成してみます。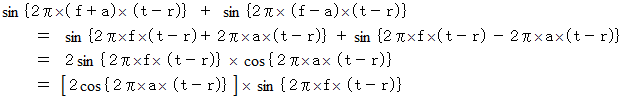
　　

　　　　

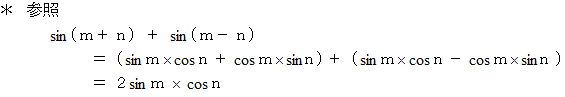
　 ここで、 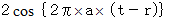を時間や距離によって変化する振幅であるとみなします。 また、 振動原点における振動のみに注目しますと、 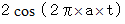となって、 時間のみによって変動する振幅とみなすことができます。 振幅は波のエネルギーの要素ですので、 音で言うと、 その大きさを決める因子になります。

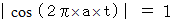　 になった後に、 次にまた 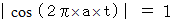になるまでの時間は次のようになります。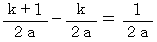
　　　　
　 以上より、 振幅は 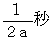間隔で大きく変動することになります。 ということは、 １秒間に 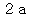回 振幅が大きく変動することになります。 これがうなりの回数です。 振動数の差が 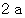で１秒間に 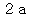回 うなるということは、「 １秒間あたりのうなりの回数は、 合成される波の振動数の差に等しい。」ということになります。 具体的に言うと、 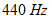と 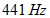では１秒間に１回うなり、 と 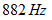では１秒間に２回うなるということです。