光が １ 秒間に伝わる距離を とし、 これを長さの単位として用いることにします。
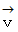　 観察者Ｂ と 被観察物質 が 観察者Ａ に対して速度 で移動しています。 この３つが１点に重なった瞬間から観察が始まります。 観察者Ａ が被観察物質を の時間観察しました。 時刻 に被観察物質の存在する時空点の座標は 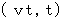で表されます。 この間、 観察者Ｂ が被観察物質を観察した場合、 最終的に被観察物質が存在する時空点の座標は 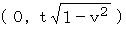になりますが、 これは、 次のようにローレンツ変換をして求めます。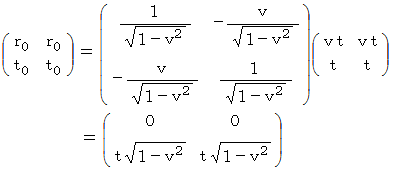
　　　　　

　 このことから「 観察者Ｂ の慣性系の時 」は「 観察者Ａ の慣性系の時 」に比べて 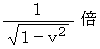ゆっくりと経過するというのが定説です。

　 しかし、 ある賢い人は次のように考えます。
「 実際の時間は、 ２つの慣性系で同じである。 観察者Ｂ の慣性系の時間の単位の長さが観察者Ａ の慣性系の時間の単位の長さに比べて 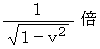長くなっているために、 座標値としてはその逆で 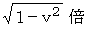になっているのだ。」

　 説得力があります。 でも、「 実際の時間は２つの慣性系で同じである。」というところは賛成ですが、 どうして２つの慣性系で時間の単位 (秒) の長さが変わるのでしょうか？　すると、 その賢い人はこう答えます。
「 それは、 そう考えると辻褄が合うからだよ。 辻褄が合うということは、 その考えが正しいということだよ。」

　 そうです、 その賢い人は「 論理実証主義者 」なのです。 それに対して私のような「 唯物論的実在主義者 」は「 それでは証明になってないよ。」と反論します。「 ローレンツ変換では、 時間や空間の単位の長さは変化しない。」というのが定説であり、 私もそうだと思います。