この法則は「物質に向心力や遠心力以外の力が作用しない限り、物質の運動量モーメントは変化しない」というものです。

　　　物質の質量： m
　　　回転中心からの位置： r(→)
　　　物質に作用する力： F(→)
　　　物質に作用する力モーメント(トルク)： N(→)
　　　物質の運動量モーメント： L(→)

この法則を導くには、物質の運動量モーメントを微分すればいいだけです。
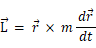　　　　　　　コメント： × は外積を表す。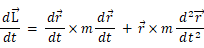
　　　
　　　
　　　
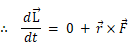
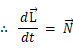
したがって、
　　　

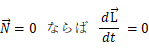
　力モーメント(トルク)： N(→) が０である場合とは、力の大きさが０ または 力の向きが力点の回転中心からの方向に平行である ときです。

　運動量モーメント保存の法則は、ケプラーの第２法則（ 面積速度一定の法則 ）を一般化したものです。 面積速度に物質の質量をかけて２倍すると物質の運動量モーメントの大きさになります。外積の大きさは平行四辺形の面積で表され、平行四辺形は２つの合同な三角形が合体したものだからです。

　この法則は質点の移動における法則であり、剛体力学ではありませんが、剛体の角運動量保存の法則とよく混同されるため、あえてここに掲載させていただきました。

　質点の角運動量保存の法則 は 剛体の角運動量保存の法則 とよく混同されるため、私は、質点の角運動量保存の法則 のことを 運動量モーメント保存の法則 と言っています。

　剛体の角運動量保存の法則については、剛体力学 ＞ 剛体の回転運動 の（２）の �C をご覧ください。