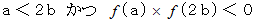 ならば、
ならば、  と
と 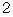
 との間に
との間に 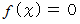 の解が1個以上存在します。 そこで、 次に
の解が1個以上存在します。 そこで、 次に  と
と 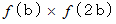 を求めます。 そして次のことが言えます。
を求めます。 そして次のことが言えます。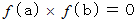 ならば、
ならば、  は
は 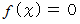 の解である。
の解である。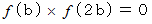 ならば、
ならば、  は
は 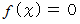 の解である。
の解である。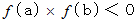 ならば、
ならば、  と
と  との間に
との間に 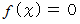 の解が1個以上存在する。
の解が1個以上存在する。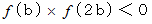 ならば、
ならば、  と
と 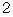
 との間に
との間に 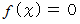 の解が1個以上存在する。
の解が1個以上存在する。このような原理を利用して、
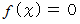 の解を求めるプログラムを作ることができます。 このプログラミングのテクニックは 「 挟みうち法 」 または 「 二分法 」 と言われます。 次のプログラムは3次方程式の解を求める 十進BASIC のプログラムです。
の解を求めるプログラムを作ることができます。 このプログラミングのテクニックは 「 挟みうち法 」 または 「 二分法 」 と言われます。 次のプログラムは3次方程式の解を求める 十進BASIC のプログラムです。http://homepage3.nifty.com/imura/index.htm
参考: 大学生のための数学 > プログラミング > 数値解析の近似値アルゴリズム
にある ニュートン法 も 挟みうち法 と同じ、
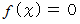 の解を求めるプログラムです。
の解を求めるプログラムです。たとえば、
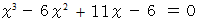 の解をこのプログラムを用いて求めてみましょう。 調査する
の解をこのプログラムを用いて求めてみましょう。 調査する  の範囲を −4 から 4 の範囲にしてください。 すると、
の範囲を −4 から 4 の範囲にしてください。 すると、 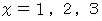 の3つの解が出力されます。 次に、
の3つの解が出力されます。 次に、 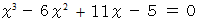 の解をこのプログラムを用いて求めてみましょう。 調査する
の解をこのプログラムを用いて求めてみましょう。 調査する  の範囲を −4 から 4 の範囲にしてください。 すると、
の範囲を −4 から 4 の範囲にしてください。 すると、 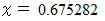 の1つの解が出力されます。 この解は近似値です。
の1つの解が出力されます。 この解は近似値です。最後に、
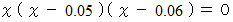 つまり、
つまり、 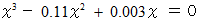 の解をこのプログラムを用いて求めてみましょう。 残念ながら
の解をこのプログラムを用いて求めてみましょう。 残念ながら 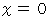 の解だけしか出力してくれません。その理由は、次の命題が真ではないからです。
の解だけしか出力してくれません。その理由は、次の命題が真ではないからです。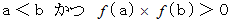 ならば、
ならば、 と
と  との間に
との間に 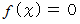 の解は存在しない。
の解は存在しない。次のプログラムは、 挟みうち法によって連立方程式の解の近似値を求めるものです。
 十進
十進