【 問 題 】

　２次元直交座標系上に３点 A, B, C があり、それぞれの位置ベクトルを 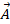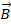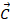，， で表すとき、次の式たちが成り立っている。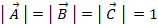
　　　　
　　　　
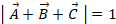
　このとき、３点は、原点を中心とする半径１の円周上にあり、かつ、そのうちの２点を結ぶ線分は円の直径になっていることを証明せよ。
　なお、位置ベクトルとは、原点を起点とし点を終点とするベクトルのことである。

【 解 答 】

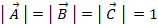　　より、３点は、原点を中心とする半径１の円周上にあることが分かる。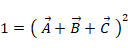
　
　　
　　　　
　　　　　　
　　
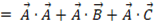
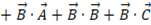
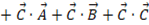
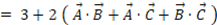
したがって、
　　
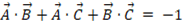
よって、
　　
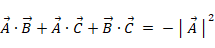
よって、
　　
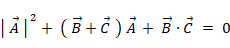
よって、
　　
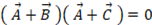
したがって、
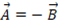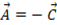　　　または　　または　

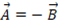　　の場合は、点A と 点B を結ぶ線分は円の直径になっていることが分かる。
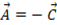　　の場合は、点A と 点C を結ぶ線分は円の直径になっていることが分かる。
　　の場合は、３点は同一円の円周上にあり、かつ、点B と 点C を結ぶ線分は円の直径になっていることがわかる。その理由は 、大学生のための数学 ＞ 幾何学 ＞ 円周角の定理を使おう　を参照のこと。

　というわけで、３点は、原点を中心とする半径１の円周上にあり、かつ、そのうちの２点を結ぶ線分は円の直径になっていることが証明された。