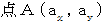 と
と 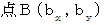 と
と 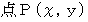 とがある。
とがある。点A と 点B と 点P の位置ベクトルをそれぞれ
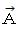 ,
, 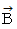 ,
, 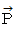 とする。
とする。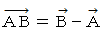 です。
です。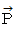 と
と 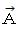 と
と 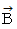 を使って式を作ってみます。 ただし、 t を任意の実数とします。
を使って式を作ってみます。 ただし、 t を任意の実数とします。(1) 点P が、 傾きが
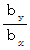 で 点A を通る直線上にある場合
で 点A を通る直線上にある場合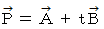
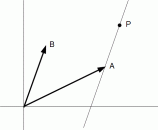
(2) 点P が、 点A と 点B を結ぶ直線上にある場合
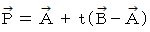
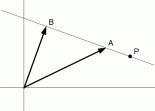
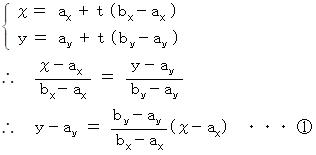
 が 点A と 点B を結ぶ直線の方程式です。
が 点A と 点B を結ぶ直線の方程式です。(3) 点P が、 点A と 点B を結ぶ直線に垂直で原点を通る直線上にある場合
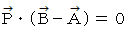
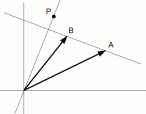
(4) 点P が、 点A を中心とする半径 r の円周上にある場合
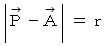
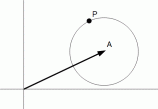
(5) 点P が、 点A と 点B を直径の両端とする円周上にある場合
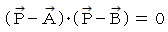
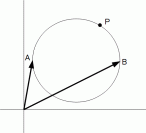
(6) 点P が、 点A と 点B を焦点とする 長軸の長さが L の楕円上にある場合
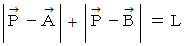
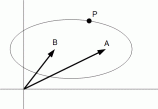
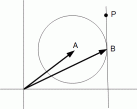
(7) 点P が、 点A を中心とする円周上の 点B における接線上にある場合
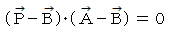
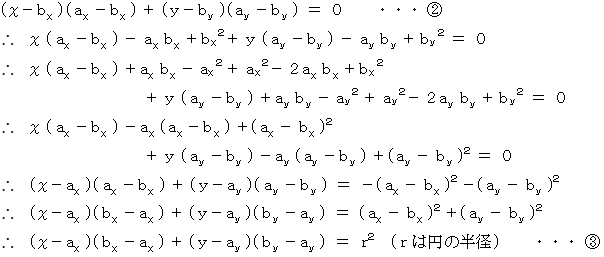
 と
と  が 点A を中心とする円周上の 点B における接線の方程式です。
が 点A を中心とする円周上の 点B における接線の方程式です。 ベクトル解析 へ戻る
ベクトル解析 へ戻る