（１） 点Ａ( a，b ) を通り、 ＯＡ(―→) ( a，b ) に垂直な直線の方程式

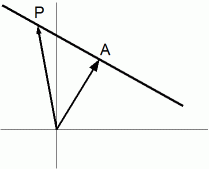
この直線上に点Ｐ( x, y, z ) を取ると、ＡＰ(―→) と ＯＡ(―→) は垂直だから、内積が０になるので、次の式が成り立ちます。
　　　a ( x − a ) + b ( y − b )　＝　0
　　　よって、　a x + b y ＝ a²＋b²
これが直線の方程式です。

　　　　　

（２） 点Ａ( a，b ) と 点Ｂ( c，d ) を結ぶ直線上の点の位置ベクトル

　　　　　

　　　　　

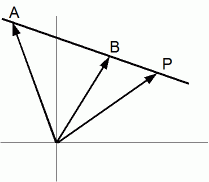
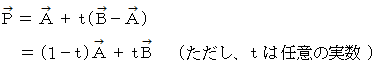
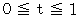　 のときは、 線分ＡＢになります。
そして、 点Ｐは線分ＡＢを　ｔ ： １− ｔ　に内分する点になります。

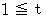　 のときは、 点Ｂを端点とする半直線になります。
そして、 点Ｐは線分ＡＢを　ｔ ： ｔ −１　に外分する点になります。