あなたに対して、 あなたのお友達が一定のリズムで踊りながら近づいてきています。 相対性理論の定説では、 あなたが見るお友達の踊りのリズムに比べて、 実際にお友達が踊っているリズムは速いということになっています。 しかし、 私はこう考えます。

　「 お友達による、 お友達についての、 当事者的な主観的観察（ Ａ ）」におけるお友達の踊りのリズムの速さ。「 あなたによる、 お友達についての、 第３者的な主観的観察（ Ｂ ）」におけるお友達の踊りのリズムの速さ。「 あなたによる、 お友達についての、 当事者的な客観的観察（ Ｃ ）」におけるお友達の踊りのリズムの速さ。 これらはすべて同じです。


　「 第３者的観察 」とは、 観察の対象物が移動しているとする立場からの観察であり、「 当事者的観察 」とは、 観察の対象物が移動していないとする立場からの観察です。
　 また、「 あなたによる主観的観察 」とは、 あなたの携帯している時計を用いて行われる観察のことであり、「 あなたによる客観的観察 」とは、 お友達が携帯している時計を用いて行われる観察のことです。
　 なお、 特殊相対性理論の定説とは異なり、 私は「 あなたによる主観的観察 」と「 あなたによる客観的観察 」は同じものであると考えています。


　 特殊相対性理論の定説では、「 あなたによる、 お友達についての、 第３者的な主観的観察（ Ｂ ）」 から 「 あなたによる、 お友達についての、 当事者的な客観的観察（ Ｃ ）」 への座標変換によって、 本来変化する「 相対的な時間（ ４次元時空間の構成要素としての時間 ）」を変化しないものであるとするために、「 本来の意味での時間（ ４次元時空間距離 ）」の長さが逆に変化する（ 具体的には縮みます ）ことになります。 そしてさらに、 特殊相対性理論の定説は、「 あなたによる、 お友達についての、 第３者的な主観的観察（ Ｂ ）」 から 「 あなたによる、 お友達についての、 当事者的な客観的観察（ Ｃ ）」 への座標変換のことを、「 あなたによる、 お友達についての、 第３者的な主観的観察（ Ｂ ）」 から 「 お友達による、 お友達についての、 当事者的な主観的観察（ Ａ ）」 への座標変換であるとしますので、「 あなたからお友達への座標変換により、 時間が縮む。」という結論に至ってしまいます。 すると、 座標変換によって観察している物の活動内容は変化しませんので、「 あなたからお友達への座標変換により、 お友達の踊りのスピードが速くなる。」ということになります。


　　コメント ：
　　　　　アインシュタインの特殊相対性理論の基本となる式は次のようになっています。
　　　　　　　　
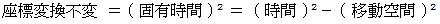
　　　　これは、（ 時間 ）^２ ＝（ 移動空間 ）^２ ＋（ 固有時間 ）^２　と書くことができます。
　　　　さらに、 座標変換不変 ＝（ 時間 ）^２ ＝（ 移動空間 ）^２ ＋（ 移動時間 ）^２　とするの
　　　　はいかかでしょうか？　アインシュタインは「 ４次元時空間の構成要素としての時間 」
　　　　と「 ４次元時空間距離としての時間 」との取り違えをしているように思うからです。