分け合う場合の数
 確率 へ戻る
確率 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2019.11.17____
【 問 題 1 】
10個の区別のつかないミカンを4人で分け合う方法について、
(1) 1人が少なくとも1個 もらうという条件では、何通にあるか?
(2) 1個ももらわない人があってもいいという条件では、何通りになるか?
【 解 答 】
(1)
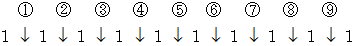
その場合の数は、9個の楔から3個の楔を選ぶときの組み合わせの数と同じです。
つまり、 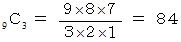 通り になります。
通り になります。
(2)
答えは、10個のミカンと3個の楔の計13個を一列に並べる場合の数です。
それは、13個の席から楔が着く3個の席の組み合わせの数と同じです。
したがって、 13C 3 = 858 通り です。
【 問 題 2 】
6m 個 の区別がつかないボール を 3つの区別がつかない箱 に入れる場合、 何通りあるか?
ただし、 一個もボールが入らない箱があってもよいものとする。
( 東大 1996年後期 入試問題より )
【 解 答 】
3つの箱を区別するとしたときの、 分け合うすべての場合の数 ( 空き箱になることもありうる ) は次のようになります。
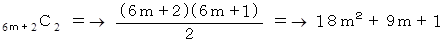
3つの箱を区別するとしたきのすべての場合の数は、 6m 個 の区別のない 〇 と2個の区別のない楔を一列に並べるすべての場合の数に等しいのです。 そしてそれは、 6m+2 個 の区別のある 位置( 席 ) から 2個の 位置( 席 ) を選ぶ 「 組み合わせ 」 に等しいです。 したがって、 3つの箱を区別するときのすべての場合の数は上記のようになるのです。
3つの箱を区別するとしたき、
3箱ともボールの数が同じときは、 ( 2m,2m,2m ) の 1 とおりです。
2箱だけボールの数が同じときは、 ( 0,0,6m ), ( 1,1,6m−2 ), ( 2,2,6m−4 ), ・ ・ ・ ・ ,( 3m,3m,0 ) の 3m+1 とおり から ( 2m,2m,2m ) の 1 とおり を除いた 3m とおり を 3倍 ( 3C2 倍 ) した数 3m × 3 とおり です。
3箱ともボールの数が異なるときは 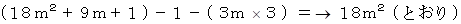 です。
です。
3箱ともボールの数が同じ場合、3つの箱を区別するときは、 3つの箱を区別しないときの場合の数と同じです。
2箱だけボールの数が同じ場合、 3つの箱を区別するときは、 3つの箱を区別しないときの場合の数の 3倍 ( 3C2 倍 ) になっています。
3箱ともボールの数が異なる場合、 3つの箱を区別するときは、 3つの箱を区別しないときの場合の数の 6倍 ( 3P3 = 3! 倍 ) になっています。
したがって、 3つの箱を区別しないときのすべての場合の数は、 次のようになります。
1 + ( 3m × 3 ) ÷ 3 + 18m2 ÷ 6 =→ 3m2 + 3m + 1 ( とおり )
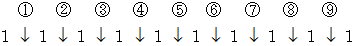
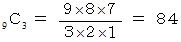 通り になります。
通り になります。 確率 へ戻る
確率 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る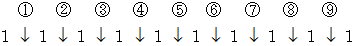
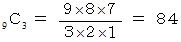 通り になります。
通り になります。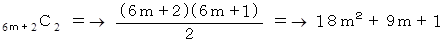
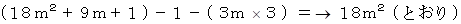 です。
です。