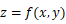は曲面の方程式です。
この曲面と x y 平面とで挟まれる部分の体積は、次の二重積分で表されます。
　　　
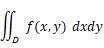
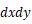は x y 平面上の微小正方形面積に相当し、 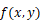は微小直方体の高さに相当します。
x, y が次のような関数によって媒介表示されるとき、
　　　x = x ( u, v )　　　y = y ( u, v )
曲面と x y 平面とで挟まれる部分の体積は、次の二重積分で表されます。
　　　
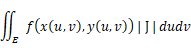
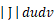は x y 平面上の微小平行四辺形面積に相当し、 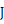は ヤコビアン と言われます。

　x y 平面上の図

　　　
　　　　　　
　　　　　　
　　　　　　

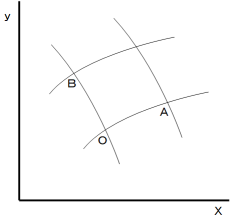
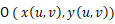
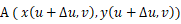
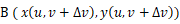
OA() と OB() が張る平行四辺形の面積は、OA() と OB()　の外積の大きさに等しく、
それは、OA() と OB() のベクペア（私の造語）の行列式の大きさに等しいのです。
OA() と OB() のベクペアは次のようになります。
　　　
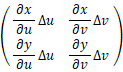
このベクペアの行列式は次のようになります。
　　　
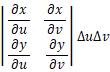
次のように置くと、
　　　
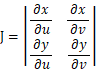
OA() と OB() が x, y 平面上に張る微小平行四辺形の面積は 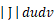になります。
これがヤコビアンの正体です。

　※ 参考： 大学生のための数学 ＞ 線形代数学 ＞ 位置ベクトルの座標変換