同じ大きさの正方形のタイルが 個あります。 すべてのタイルを、 次の条件にしたがって、 上から下へと敷き詰めていきます。
　　　　上辺と左辺が揃っていること。
　　　　下段は上段のタイル数を超えないこと。
　　　　隙間なく敷き詰めること。
何とおりの方法があるでしょうか？

　 この問題は、 ある自然数 を自然数の和として展開する時に、 何通りあるのかという問題と同じです。 自然数を自然数の和として展開することを 「 自然数を分割する 」 と言いますので、 「 自然数 の分割の方法は何通りあるか？　ただし、 分割しない場合も１通りとする。」 という問題と同じことになります。 またこの問題は 「 自然数 の分割数はいくつか？」 という言い方をされます。

　 では、 「自然数 の分割数はいくつか？」 を求めていくことにしましょう。 まず、 「 自然数 を 個に分割する方法は何通りあるか？」 を考えることにします。 たとえば、 ９を３個に分割すると、 次の５通りになります。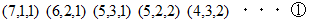
　　　　　
　 次に９を４個に分割することを考えますと迷宮に入りますので、 １０を４個に分割することを考えることにします。 すると、 次の７通りになります。
　　　　　
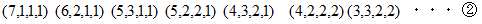
　 と の第５番目まで をそれぞれ比べてみましょう。 のカッコの中の数字の一番右に が付け加えられたものが になっています。
　 その次に、 ６を４個に分割することを考えることにします。 すると、 次の２通りになります。
　　　　　
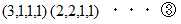
　 の第６番目以降 と をそれぞれ比べてみましょう。 のカッコの中の数字にすべて を加えたものが になっています。

　以上より、 １０を４個に分割する方法の数は、 ９を３個に分割する方法の数 と ６を４個に分割する方法の数 を加えたものであることが解ります。 こうして、 一般的に次の漸化式が成り立っていることに気づきます。 自然数 を 個に分割する場合の数を 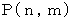とすると、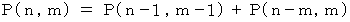
　　　　　

　 したがって、 「 自然数 の分割の方法は何通りあるか？」 という問題に答えるためには、 上記の式の を から まで１つずつ増やしていってその総計をとればいいことになります。

　 このアルゴリズムを用いて作られたのが、 次の十進BASIC のプログラムです。

　　　　　このプログラムソースは、 山中和義 / 電脳遊戯団 さんよりいただきました。
　　　　　　　　　　http://www.urban.ne.jp/home/kz4ymnk/seminar/basic/

　 このプログラムソースもまた、 山中和義 / 電脳遊戯団 さんよりいただいたのですが、 具体的な分割方法とそれに対応するヤング図形をすべて出力してくれるプログラムを以下に紹介させていただきます。