（１） 楕円の定義

　x y 座標系に、点Ｆ( 4，0 ) と 直線Ｌ： x ＝ 25/4 があります。
前者との距離と後者との距離の比が 4：5 になる点Ｐ ( x，y ) の集まりは、どんな方程式で表せるでしょうか？

点Ｐと点Ｆとの距離の２乗 (Ａ)： ( x − 4 )² ＋ y²
点Ｐと直線Ｌとの距離の２乗 (Ｂ)： ( 25/4 −x )²
Ａ×25 ＝ Ｂ×16　だから、
　　25 x² − 200 x ＋ 400 ＋ 25 y²　＝　16 x² − 200 x ＋ 625
よって、
　　9 x² ＋ 25 y² ＝ 225
よって、
　　

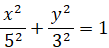
この方程式は楕円を表します。 長径が x 軸上にあり、短径が y 軸上にあり、中心が原点にある楕円です。点Ｆは焦点です。

　　　　


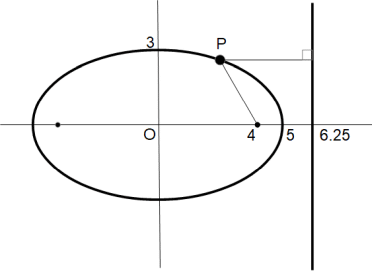
（２） 楕円の性質

　次の方程式で表される楕円があります。
　　　
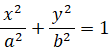
　この楕円は、長径が x 軸上にありその長さが 2a で、短径が y 軸上にありその長さが 2b で、中心が原点にあります。

　　　　

　　　　
　　
　　

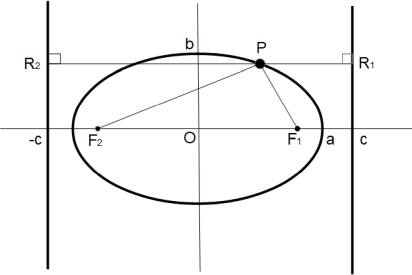
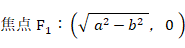
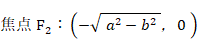
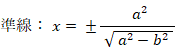
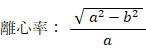
「 楕円上の点は、２つの焦点からの距離の和が長径に等しくなっており一定である。」ことは、次の３つの式から導かれます。
　　
　　
　　
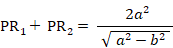
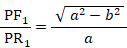
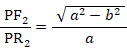
よって、
　　
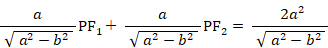
よって、
　　


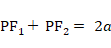
　「 楕円の離心率を求めるには、２つの焦点間の距離を長径で割ればいい。」ことは、離心率の分子・分母を２倍するとわかります。

　楕円の扁平率 ＝ ( 長径 − 短径 ) ÷ 長径　であり、離心率より扁平率の方が楕円の形をイメージしやすいと思います。
　短径/長径比 ( b/a ) を用いると、楕円の扁平率は次の式で表されます。
　　　楕円の扁平率 ＝ １− b/a