(1) 破産ゲーム その1
-
A君は m 円、 B君は n 円 持っています。 じゃんけんをして負けた方は勝った方に 1 円 渡します。 どちらかの所持金がなくなるまで続けます。 B君が破産する確率はいくらですか?
B君の所持金が k 円 のとき、 B君が破産する確率を Pk とします。 すると、 次の漸化式が成り立ちます。
Pk = 1/2 × Pk+1 + 1/2 × Pk-1 ・ ・ ・ ・

( P0 = 1 , Pm+n = 0 )
 より、 Pk+1 - Pk = + Pk - Pk-1
より、 Pk+1 - Pk = + Pk - Pk-1ゆえに、 Pk は 等差数列である。 公差をSとすると、
Pk = S×k + 1 ( k = 0,1,2,・ ・ ・ )
Pm+n = 0 より、 0 = S( m+n ) + 1
よって、 S = -1 /( m+n )
よって、 Pk = -k /( m+n )+ 1
よって、 Pn = -n /( m+n )+ 1 =→ m /( m+n)
これが答えになります。
-
【 問 題 】
-
最初に1円が与えられる。その後にコイントスして表が出れば2円もらえ、裏が出れば1円を失う。これを繰り返して行くのだが、手持ちのお金が無くなった時点でゲームセットである。永遠にゲームが続く確率を求めよ。
-
1円を持っているときにゲームセットになる確率は、2円を持っているときに手持ちのお金が1円になる確率と等しく、3円を持っているときに手持ちのお金が2円になる確率と等しく、4円を持っているときに・・・・。
というわけで、1円を持っているときにゲームセットになる確率を P1、n 円を持っているときにゲームセットになる確率を Pn とすると、次の式が成り立つ。
Pn = P1n ・・・ ①
一方、次の漸化式が成り立たつ。
Pn = (1/2) Pn-1 + (1/2) Pn+2 ・・・ ②
①を②に代入して、
P1n = (1/2) P1n-1 + (1/2) P1n+2
よって、
2 P1n+1 = P1n + P1n+3
よって、
2 P1 = 1 + P13
よって、
P13 - 2 P1 + 1 = 0
よって、
( P1-1 ) ( P12+P1-1 ) = 0
よって、
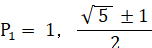
0 < P1 < 1 だから、
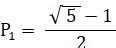
したがって、答えは、1から P1 を引いて、
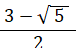 ( ≒ 0.382 )
( ≒ 0.382 )コンピューターシミュレーション:
プログラムの内容 :
(3) 破産ゲーム その3
-
9円持っています。 1秒ごとに 1 ~ 20 の自然数から無作為に1つ選び、 9以下ならば 1 円失い、 10以上ならば 1 円 取得します。 0円になったら負け、 20円になったら勝ち、 10分たっても決着がつかなければ引き分けとします。 負ける確率は何%でしょう? 1万回試行してみます。
思ったよりも負ける確率は少なかったのではないでしょうか?
この問題は 「 破産の確率 」 と言われ、 最後まで決着をつける場合は、 確率漸化式から理論的に答えを求めることができますので、 やってみましょう。
最初に n 円 持っているときに負ける確率を
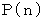 とすると、
とすると、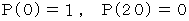
第1回目に1円取得する確率に1円取得した直後における負ける確率をかけたもの と 第1回目に1円失う確率に1円失った直後における負ける確率をかけたもの とを加えたものは、 まだ勝負が始まっていないときの最初に n 円 持っているときに負ける確率に等しいので、 次の式が成り立つ。
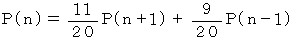
第2回目以降も同様になるので、 一般に上式は成り立つ。
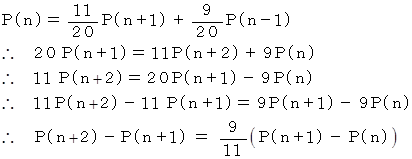
したがって、
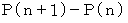 は、 初項
は、 初項 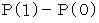 、 公比
、 公比 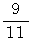 の n = 0 から始まる 等比数列であることがわかる。 したがって、
の n = 0 から始まる 等比数列であることがわかる。 したがって、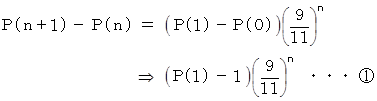
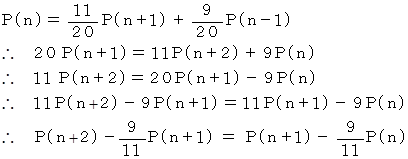
したがって、
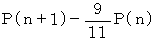 は、 初項
は、 初項 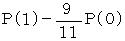 、 公比 1 の n = 0 から始まる 等比数列であることがわかる。 したがって、
、 公比 1 の n = 0 から始まる 等比数列であることがわかる。 したがって、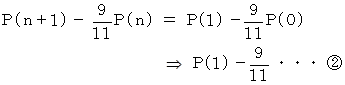
 から
から  を 辺々ひくと、
を 辺々ひくと、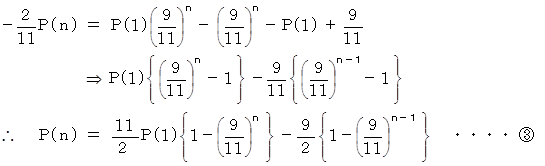
n = 20 のとき、
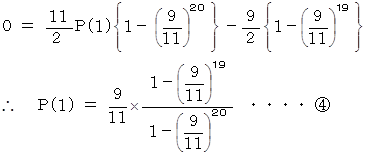
 を
を  に代入して、
に代入して、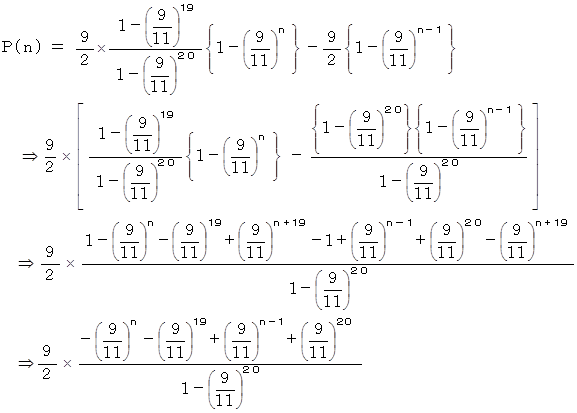
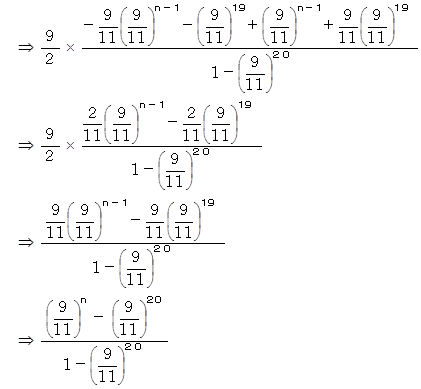
 確率 へ戻る
確率 へ戻る