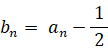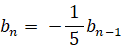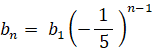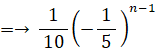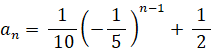次の漸化式が成り立つ。
ｎ ＝ １ ： an ＝ 3/5
ｎ ＞ １ ： an ＝ an−1 × 2/5 ＋ ( １−an−1 ) × 3/5
＝→ −1/5 an−1 ＋ 3/5
an ＝ −1/5 an−1 ＋ 3/5 は次のように変形できる。
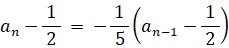
参照： 数理論 ＞ 解ける漸化式づくりのための特性方程式ここで、次のように置く
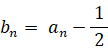
すると次のようになる。
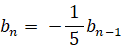
bn は 初項 b1 公比 −1/5 の等比数列だから、
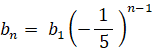
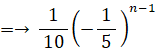
よって、
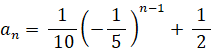
10万回のシミュレーション：
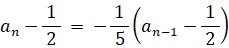
確率 へ戻る 大学生のための数学 へ戻る 参照： 数理論 ＞ 解ける漸化式づくりのための特性方程式