（１） 見かけの大きさ

　 半径 の球の表面を円形に切り取った面積 の皿状曲面Ａがあります。 皿状曲面Ａの焦点までの距離は です。 皿状曲面Ａの焦点を頂点とする円錐様立体の頂点の立体角は１ステラジアンです。 半径 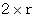の球の表面を円形に切り取った面積 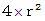の皿状曲面Ｂがあります。 皿状曲面Ｂの焦点までの距離は 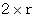です。 皿状曲面Ｂの焦点を頂点とする円錐様立体の頂点の立体角は１ステラジアンです。 立体角が等しい時、 皿状曲面の面積は、 距離の２乗に比例します。 ということは、 皿状曲面の直径は観察者からの距離に比例します。

　　　　　　　　　焦点とは、 ある点光源から放たれた光または平行光線（ 点光源が無限
　 　　　　　　　の距離はなれている場合 ）が屈折や反射によって１点に集まる場合の光の
　 　　　　　　　集まる点のことをいいます。
　　　　　　　　　　ちなみに、 レンズの焦点とは、 平行光線が１点に集まる場所のことです。

　 立体角は物質の「 見かけの大きさ 」を表します。 視覚的な意味で円や球の大きさを表すのは面積や体積ではなく直径です。 なぜなら、 文字の大きさを２倍に拡大するということは、 縦や横の長さを２倍ずつ大きくするということだからです。 したがって、 バケツの絵を見て、「 こっちのバケツのほうが２倍大きい。」と表現されるような場合は、「 こっちのバケツの容量は８倍大きい。」ということを表していることがほとんどです。 しかし、 実際のバケツを手にとって見た時は、 人はそれを８倍の大きさの差と表現するかもしれません。

　 ２つの物質の大きさを比較するときは「 見かけの大きさ 」ではなく「 実際の大きさ 」で比較すべきですが、「 見かけの大きさ 」からでも比較することができます。 ただし、 それは２つの物質が観察者から同じ距離の所に存在しているか、 または、 ２つの物質の観察者からの距離の比率がわかっていることが条件になります。「 見かけの大きさ 」を等しくした場合には、「 実際の大きさ（ 直径や幅による大きさの判断 ）」の比率は「 観察者からの距離 」の比率に比例します。


　 伸縮自在の筒（ 直径３ｃｍ、 最大長55ｃｍ ）を用意して下さい。 両手を用いて仮想の筒を作ってもいいでしょう。 そして、 110ｃｍ 向こう側に、 文字がぎっしりと書かれた本を立てかけ、 その筒で覗きます。 文字を見ながら、接眼側の位置を固定し、 対物側を移動させて筒を伸ばしたり縮めたりしてみてください。 文字の大きさは変化せず視野だけが変化します。 では次に、 文字を見ながら、 筒の対物側の位置を固定し、 接眼側を移動させて筒を伸ばしたり縮めたりしてみてください。 先ほどと比べると視野の変化の程度が少なく、 文字のみかけの大きさが変化します。 本の代りにパンチコ玉でもやってみてください。 月の見かけの大きさは、 110ｃｍ 離れたパチンコ玉です。 このとき地球はピンポン玉大です。 ちなみに地球がパチンコ玉大ならば、 太陽は210ｍ先の直径１ｍの球です。

　 では、 次の実験に行きましょう。 左手の人差し指の先と親指の先の間を10ｃｍくらいに開いて固定してください。 そしたら、 両方の親指の先をくっつけて右手の人差し指を左手の人差し指の先と親指の先とでできる線分の中点に持っていって固定してください。 そこで片目をつむって、 両腕を動かし、 見かけ上、 両手の 親指と親指 ＆ 人差し指と人差し指 が接触するようにしてください。 このとき、 眼からの距離は、 左手が右手の２倍になっていて、 指の太さは、 右手が左手の２倍になっています。 ピントを右の人差し指にしたり左の人差し指にしたりしてみてください。

（２） 視野

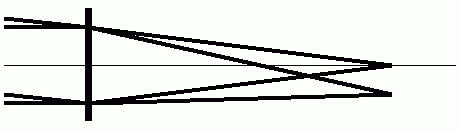
　 南中した満月の真ん中にピントをあわせて見た時、 網膜には、 黄斑部中心窩を中心とする小さな上下左右反対の月の実像が映っています。 満月の真ん中の点で跳ね返った太陽光は直径100ｍの円柱空間の中を伝わる平行光線のイメージで、 自分の眼のレンズの中心面に対して垂直に届いていると考えてください。 また、 満月の端の１点で跳ね返った太陽光は直径100ｍの円柱空間の中を伝わる平行光線のイメージで、 自分の眼のレンズの中心面に対して垂直から少し傾いて届いていると考えてください。 これが遠方視の場合の見え方です。 遠方に存在するある点光源から放たれる光を真正面に注視したときに、 眼のレンズの中心面に対して斜めに入ってくる平行光線も網膜上で１点に集まりますが、 それは中心から外れるほどぼんやりと認識できる程度のものになります。 その見える範囲を片眼遠方視野といいます。 水平鉛直方向はほぼ等しく前方160度くらいだそうです。