光学 へ戻る（１）明視距離
-
点光源と右眼との距離が無限のとき、 右眼のレンズは最も平べったい状態で、 健常者では焦点距離がレンズと網膜との距離に等しい状態になっています。 また、 点光源と右眼との距離が
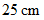のとき、 右眼のレンズは最も膨らんだ状態（ 最も焦点距離の短い状態 ）になっています。 点光源と右眼との距離が 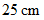未満のときは、 もう右眼の凸レンズは網膜上の１点に光を集めることができなくなっており、 点光源はボーっとしか見えていません。 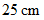は「 明視距離 」の標準値と言われます。-
光軸とは、 凸レンズの真ん中を一方の面から他方の面へと直角に貫く軸のことです。 レンズの中心を通る光は、 すべて直進します。 光軸に平行な光は、 レンズを通って屈折した後、 必ず焦点を通ります。 レンズの手前にある焦点を通る光は、 レンズを通過した後、 必ず光軸に平行に進みます。
凸レンズの焦点より遠くに存在する物質の、 同じ場所から放たれ続けるこれらの光は、 レンズを通過した後、 １つの共通する点を通ります。 上記以外のルートを通る同じ場所から放たれてレンズを通過する光もすべてその点を通過します。 そして、 物質のいろんな場所から放たれ続ける光がある場合は、 その所に物質の像ができます。 この像は、 物質が焦点距離の２倍以上凸レンズから離れているとき縮小しており、 焦点距離の２倍未満しか凸レンズから離れていないときは拡張しています。 これは、 上下左右反対の「 実像 」です。
凸レンズの焦点より近くに存在する物質の、 同じ場所から四方八方へと放たれ続ける光たちは、 レンズを通過した後に１つの共通する点を通りません。 しかし、 その光をレンズを通して見ると、 実際の位置よりも遠く、 また、 光軸からより離れた所から、 放出され続けているように見えます。 そして、 物質のいろんな場所から放たれ続ける光がある場合は、 その所に物質の拡大された像ができます。 これは、 上下や左右が反対ではない「 虚像 」です。 虚像の位置は、「 レンズの中心を通る光の軌道 」と「 光軸に平行な光の レンズを通って屈折した後の軌道 」との交点になります。
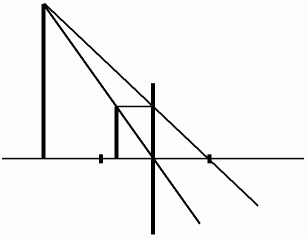
「 虚像の拡大率 」を求めてみましょう。 凸レンズの焦点距離を
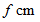とし、 凸レンズから 
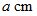の位置に光軸上から垂直方向に棒を立てます。「 虚像の棒の長さ 」の「 実物の棒の長さ 」に対する比率が「 虚像の拡大率 」になります。
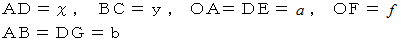
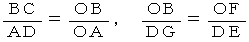
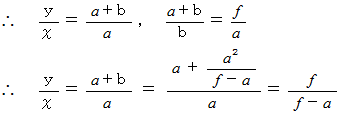
したがって「 虚像の拡大率 」は次のようになります。
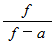（ f ＝ 焦点距離 a ＝ 観察物のレンズからの距離 ）この式より、「 虚像の拡大率 」は
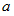が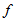 
に近づくほど大きくなって、 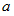が 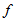に等しくなると無限大になることがわかります。 
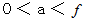なので、 この式をさらに変形します。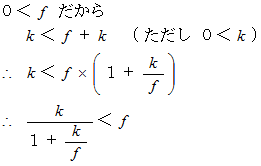
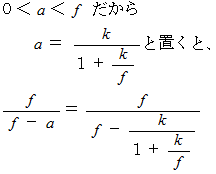
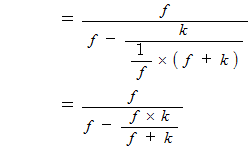
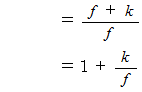
凸レンズの「 虚像の拡大率 」は物質の位置によって変化することはわかりましたが、 上記の「 虚像の拡大率 」を表す式において、 任意の正の実数
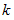を特定な値にしたときの「 虚像の拡大率 」の値を示すことによって、 そのレンズの拡大能力を表すことができます。 これが「 凸レンズの倍率 」という概念です。 そして、 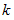を「 明視距離 」の標準値としたときの「 虚像の拡大率 」 を「 凸レンズの倍率 」ということになりました。 焦点距離が無限大のレンズの倍率が １ になり、 焦点距離が「 明視距離 」の標準値に等しいレンズの倍率が２になるようにしたのです。したがって、「 凸レンズの倍率 」の定義は次のようになります。
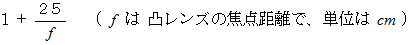
ちなみに、
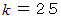のとき、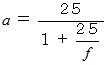
ですから、 
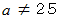です。凸レンズの倍率とは、 凸レンズから
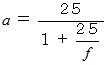（ 単位は ｃｍ ）の距離だけ離して物体を置いた時の「 虚像の拡大率 」である、 とも言えます。 倍率とは 25cm 離れた状態で対象物を見たとき、 対象物が何倍に拡大されて見えるかではありません。 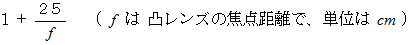を変形すると、 
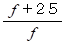になりますので、 凸レンズの倍率は次の式でも表わすことができます。