数理論 へ戻る(０) 10進数の整数を２進数に変換する方法
-
十進数の13を２進数に直します。 まず13を２で割って商と余りを求めます。 商が６で余りが １ です。 そこで下から １ 桁目の数は １ であることが解ります。 次に６を２で割って商と余りを求めます。 商が３で余りが０です。 そこで下から２桁目の数は０であることがわかります。 次に３を２で割って商と余りを求めます。 商が １ で余りが １ です。 そこで下から３桁目の数は １ であることがわかります。 次に １ を２で割って商と余りを求めます。 商が０で余りが １ です。 そこで下から４桁目の数は１であることが判ります。 したがって、 ２進数では 1101 です。 確かめてみましょう。
-
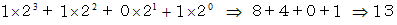
10進数の小数部分を２進数に変換するには、２をかけては整数部分を引き、 またそれに２をかけては整数部分を引き、 ・ ・ ・ ・ というふうにします。
【 例 題 】
-
10進数の 0.35 を２進数に変換しなさい。
-
0.35 × 2 ＝ 0.7
0.7 − ０ ＝ 0.7
0.7 × 2 ＝ 1.4
1.4 − １ ＝ 0.4
0.4 × 2 ＝ 0.8
0.8 − ０ ＝ 0.8
0.8 × 2 ＝ 1.6
1.6 − １ ＝ 0.6
0.6 × 2 ＝ 1.2
1.2 − １ ＝ 0.2
0.2 × 2 ＝ 0.4
0.4 − ０ ＝ 0.4
0.4 × 2 ＝ 0.8
0.8 − ０ ＝ 0.8
0.8 × 2 ＝ 1.6
1.6 − １ ＝ 0.6
0.6 × 2 ＝ 1.2
1.2 − １ ＝ 0.2
0.2 × 2 ＝ 0.4
0.4 − ０ ＝ 0.4
0.4 × 2 ＝ 0.8
0.8 − ０ ＝ 0.8
0.8 × 2 ＝ 1.6
1.6 − １ ＝ 0.6
・
・
・
したがって、 10進数の小数 0.35 を２進数に変換すると、 次のようになります。
0.010110011001100・・・・
では、 上記の２進数を10進数に変換して、 0.35 に戻るかどうか確かめてみましょう。
0.010110011001100・・・・ ＝ 0.010 ＋ 0.000110011001100・・・・
0.01 ( ２進数 ) → (1/2) 2 ( 10進数 ) → 0.25 ( 10進数 )
0.000110011001100・・・・ を10進数に変換すれば a になるものとすると、
0.000110011001100・・・・ ( ２進数 )
→ a ( 10進数 ) ＝ (1/2) 4 ＋ (1/2) 5 ＋ (1/2) 8 ＋ (1/2) 9 ＋ (1/2) 12 ＋ (1/2) 13 ＋ ・ ・ ・ ・
( この式を
と置く ） の辺々に 2 4 をかけて、2 4 a ＝ １ ＋ (1/2) ＋ (1/2) 4 ＋ (1/2) 5 ＋ (1/2) 8 ＋ (1/2) 9 ＋ (1/2) 12 ＋ (1/2) 13 ＋ ・ ・ ・ ・
( この式を
と置く ） から を辺々引いて、15 a ＝ １ ＋ (1/2) ＝→ 1.5
よって、 a ＝ 0.1
したがって、
0.010110011001100・・・・ ( ２進数 ) → 0.25 ＋ 0.1 ( 10進数 ) ＝→ 0.35
２進数の小数 0 . a b c d ( a, b, c, d は ０ または １ )
を10進数に変換すると、
a × 2 −1 ＋ b × 2 −2 ＋ c × 2 −3 ＋ d × 2 −4
-
0.3125 ＝ 0.625 × 1/2
＝ ( 0.625 ＋ ０ ) × 1/2
＝ 0.625 × 1/2 ＋ ０ × 1/2
＝ ( 1.25 × 1/2 ) × 1/2 ＋ ０ × 1/2
＝ ( ( 0.25 ＋ １ ) × 1/2 ) × 1/2 ＋ ０ × 1/2
＝ ( 0.25 × 1/2 ＋ １ × 1/2 ) × 1/2 ＋ ０ × 1/2
＝ 0.25 × (1/2) 2 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ ( 0.5 × 1/2 ) × (1/2) 2 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ ( ( 0.5 ＋ ０ ) × 1/2 ) × (1/2) 2 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ ( 0.5 × 1/2 ＋ ０ × 1/2 ) × (1/2) 2 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ 0.5 × (1/2) 3 ＋ ０ × (1/2) 3 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ ( １ × 1/2 ) × (1/2) 3 ＋ ０ × (1/2) 3 ＋ １ × (1/2) 2 ＋ ０ × 1/2
＝ １ × (1/2) 4 ＋ ０ × (1/2) 3 ＋ １ × (1/2) 2 ＋ ０ × 1/2
したがって、 10進数の小数 0.3125 を２進数に変換すると、 0.0101 になります。
では、 ２進数 0.0101 を10進数に変換して、 0.3125 に戻るかどうか確かめてみましょう。
0.0101 ( ２進数 ） → (1/2) 2 ＋ (1/2) 4 ( １０進数 ）
＝→ 1/4 ＋ 1/16 ＝→ 5/16 ＝→ 0.3125
-
次の十進BASIC のプログラムでは 10進数の小数を10進数以下の小数に変換することができます。 ただし、 任意に行うと桁がオーバーフローしてしまいますので、 あらかじめ小数点以下10桁以下の数に変換される10進数のみを取り扱っています。
また、 次のプログラムは10進数の分数を２進数の小数に変換する十進BASIC のプログラムです。
＜ JavaScript のプログラム ＞
２進数の小数を10進数に変換した後、再び２進数に変換します。
プログラムの内容：
（４) 応用問題
-
【 問 題 】
-
10進数の 5.875 を２進数にしなさい。
-
5 ÷ ２ ＝ 2 あまり １
2 ÷ ２ ＝ 1 あまり ０
1 ÷ ２ ＝ 0 あまり １
したがって、 5 ⇒ 101
0.875 × ２ ＝ 1.75
1.75 − １ ＝ 0.75
0.75 × ２ ＝ 1.5
1.5 − １ ＝ 0.5
0.5 × ２ ＝ 1
1 − １ ＝ 0
したがって、 0.875 ⇒ 0.111
よって、 答えは 5.875 ⇒ 101.111
８ｋ ＝ 47
よって、 ２3 k ＝ ２5 ＋ ２3 ＋ ２2 ＋ ２ ＋ １
よって、 k ＝ ２2 ＋ １ ＋ ２−1 ＋ ２−2 ＋ ２−3
よって、 答えは 5.875 ⇒ 101.111