【 問 題 】

３乗すると −８ になる複素数を求めよ。

【 解 答 】

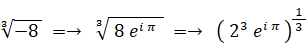
０ 以上 2π 未満で、３倍すると π または ３π または ５πになる角度は、次の３つである。
　　　
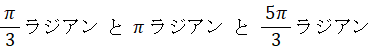
したがって、答えは、次の３つである。
　　　
　　　
　　　

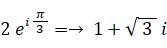
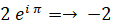
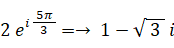
確かめ：
　　　
　　　

【 別 解 】

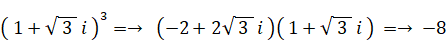
( a + bi )³ ＝ −８　と置く。

すると、
　　　a ( a²−3b² ) ＋ b ( 3a² − b² ) i　＝ −８
したがって、
　　　a ( a²−3b² ) ＝ −８
　　　　　　　かつ
　　　{ b ＝ 0　または　3a² − b² ＝ 0 }
したがって、
　　　{ a ( a²−3b² ) ＝ −８　かつ　b ＝ 0 }　　・・・ �@
　　　　　　　　　　または
　　　{ a ( a²−3b² ) ＝ −８　かつ　3a² − b² ＝ 0 }　　・・・ �A

�@ について
　　　b ＝ 0　かつ　a³ ＝ −８　　⇒　　b ＝ 0　かつ　a ＝ −2　　⇒　−2 は答えの１つ
�A について
　　　b² ＝ 3a²　を　a ( a²−3b² ) ＝ −８　に代入して、
　　　　　　−8a³ ＝ −８　　⇒　　a ＝ 1
　　　　　　b² ＝ 3a² 　に　a ＝ 1　を代入して、
　　　　　　　　　b ＝ ±root(3)　　⇒　　1 ± root(3) i　は答えの１つ