幾何学 へ戻る【 問 題 １ 】
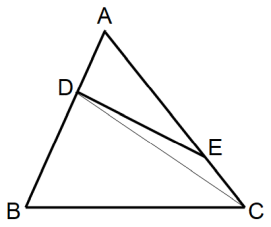
AD : BD ＝ 1 : 2
AE : CE ＝ 3 : 1
△ABC ＝ 20（ 面積 ）
△ADE の面積を求めよ。
-
△ABC : △ADC ＝ 3 : 1
△ADC : △ADE ＝ 4 : 3
したがって、
△ABC : △ADC ＝ 12 : 4
△ADC : △ADE ＝ 4 : 3
したがって、
△ABC : △ADE ＝ 12 : 3 ＝→ 4 : 1
したがって、
△ADE の面積は 5 である。
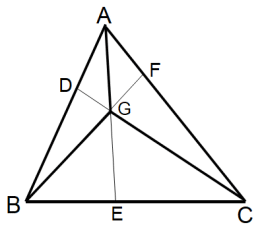
AD : BD ＝ 1 : 2
AF : CF ＝ 1 : 3
△ABC ＝ 22（ 面積 ）
△AGC, △GBC,△ABG の面積をそれぞれ求めよ。
-
△AGC : △GBC ＝ 1 : 2
なぜなら、△ADC : △BDC ＝ 1 : 2 かつ △ADG : △BDG ＝ 1 : 2
△ABG : △GBC ＝ 1 : 3
したがって、
△AGC : △GBC ＝ 3 : 6
△ABG : △GBC ＝ 2 : 6
したがって、
△AGC : △GBC : △ABG ＝ 3 : 6 : 2
したがって、
△AGC ＝ 6 , △GBC ＝ 12, △ABG ＝ 4
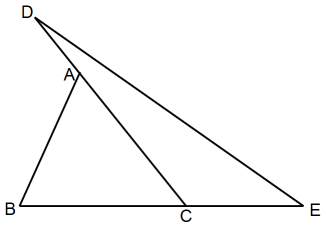
BC : CE ＝ 6 : 4
DA : AC ＝ 3 : 7
△ABC ＝ 21（ 面積 ）
△DCE の面積を求めよ。
-
△ABC と △DCE の高さの比は 7：10 である。
したがって、
△ABC : △ADE ＝ 1/2 × 6 × 7 : 1/2 × 4 × 10 ＝→ 21 : 20
したがって、
△DCE の面積は 20 である