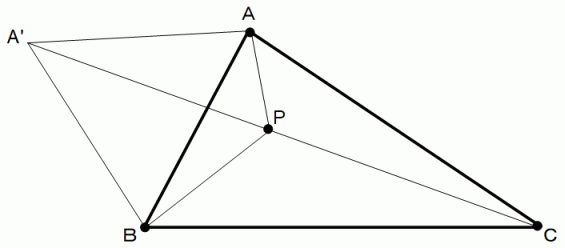
どの内角も120度未満の三角形ABC があります。 AB を底辺とする正三角形の頂点をA'とします。 三角形の中に点Pを取ります。 点Pからそれぞれの頂点への距離の合計が最短になるとき、 点Pは線分A'C 上に存在します。
 幾何学 へ戻る
幾何学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る
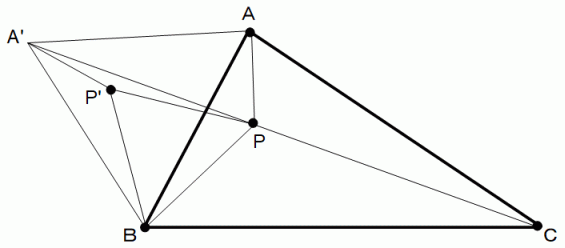


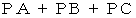 を最短にする点になっています。 点P は発見者にちなんでフェルマー点と言われますが、 そうなる理由を証明します。
を最短にする点になっています。 点P は発見者にちなんでフェルマー点と言われますが、 そうなる理由を証明します。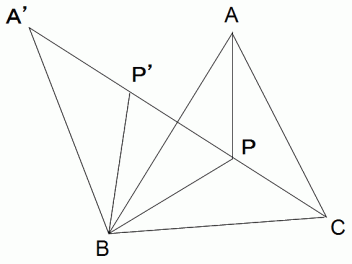
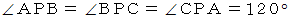
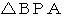 を 点B を中心にして反時計回りに60° 回転させたのが、
を 点B を中心にして反時計回りに60° 回転させたのが、 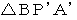 です。
です。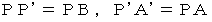 ですから、
ですから、 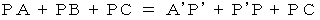 です。
です。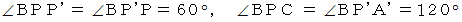 なので、
なので、 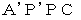 は一直線上にあります。
は一直線上にあります。 の位置は点P の位置に関係なく決まりますので、 点P の位置に関係なく
の位置は点P の位置に関係なく決まりますので、 点P の位置に関係なく 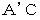 の長さは一定です。
の長さは一定です。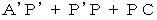 が最短になるのは、
が最短になるのは、 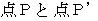 が線分
が線分 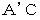 上にあるときです。
上にあるときです。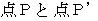 が線分
が線分 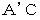 上に存在するためには、
上に存在するためには、 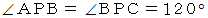 でなければなりません。 したがって、 図の場合が
でなければなりません。 したがって、 図の場合が 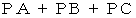 が最短になっていることが解ります。
が最短になっていることが解ります。